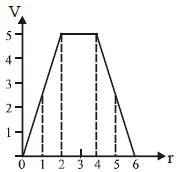
Question 8: A solid non-conducting sphere is uniformly charged through its volume. Electric potential (V) at a distance (r) from the center of the sphere can be plotted qualitatively as:
View Solution
Solution:
For a solid, non-conducting sphere uniformly charged throughout its volume, the electric potential \( V(r) \) is determined as follows:
---
Inside the sphere (\( r \leq R \)):
Using Gauss's law, the electric field inside the sphere is:
\[
E = \frac{\rho r}{3\epsilon_0},
\]
where \( \rho \) is the charge density, and \( R \) is the sphere's radius.
The potential \( V(r) \) at a distance \( r \) from the center is obtained by integrating the electric field:
\[
V(r) = V(R) - \int_r^R E \, dr = V(R) - \int_r^R \frac{\rho r}{3\epsilon_0} \, dr.
\]
Simplifying:
\[
V(r) = V(R) - \frac{\rho}{6\epsilon_0} \left( R^2 - r^2 \right).
\]
Thus, inside the sphere, \( V(r) \) is a quadratic function of \( r \), decreasing as \( r^2 \).
---
Outside the sphere (\( r > R \)):
The sphere acts as a point charge with total charge \( Q = \frac{4}{3} \pi R^3 \rho \). The potential outside is:
\[
V(r) = \frac{1}{4\pi\epsilon_0} \frac{Q}{r}.
\]
Here, \( V(r) \) decreases inversely with \( r \).

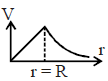
Behavior of the Graph:
1. At \( r = R \): The potential is continuous, with its value matching between the inside and outside solutions.
2. Inside the sphere (\( r < R \)): \( V(r) \) decreases quadratically as \( r^2 \).
3. Outside the sphere (\( r > R \)): \( V(r) \) decreases inversely with \( r \).
Thus, the graph shows a continuous potential that decreases quadratically inside the sphere and decreases inversely outside the sphere, matching the provided curve.
Discuss this question