A body is released from position A as shown in figure. The speed of body at position B is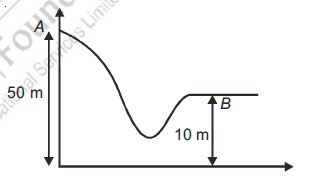
Solution:
From Principal of Conservation of Energy
Ui + Ki= Uf+ Kf
⇒ mg(50) + 0 = mg(10) + ½ m v²
⇒ v² = 800
⇒ v = 20√2 m/s
A body is released from position A as shown in figure. The speed of body at position B is
From Principal of Conservation of Energy
Ui + Ki= Uf+ Kf
⇒ mg(50) + 0 = mg(10) + ½ m v²
⇒ v² = 800
⇒ v = 20√2 m/s
A child on a swing is 1 m above the ground at the lowest point and 6 m above the ground at the highest point. The horizontal speed of the child at the lowest point of the swing is approximately
From Principal of conservation of Energy in absence of non-conservative forces,
Ui+ Ki= Uf+ Kf
⇒mg(6) +0 = mg(1) + ½mv²
⇒mg(5)= ½mv²
⇒ v²=100 or v =10 m/s
A mass m slips along the wall of a hemispherical surface of radius R. The velocity at the bottom of the surface is
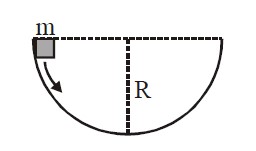
From Principal of conservation of Energy in absence of non-conservative forces,
Ui+ Ki= Uf+ Kf
mgR+0= 0+ ½mv²
v= √2gR
The block of mass M moving on the frictionless horizontal surface collides with the spring of spring constant K and compresses it by length L. The maximum momentum of the block after collision is
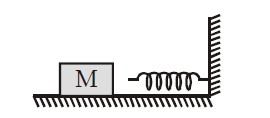
From Principal of conservation of Energy in absence of non-conservative forces,
Ui+ Ki= Uf+ Kf
½KL²+ 0 = ½mv²
⇒v= √(KL²/m)
Momentum is P= m.v = m. √(KL²/m) =(mK)½ L
A simple pendulum is released from A as shown. If m and l represent the mass of the bob and length of the pendulum, the gain in kinetic energy at B is
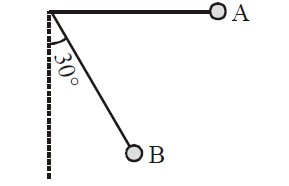
From Principal of conservation of Energy in absence of non-conservative forces,
Ui+ Ki= Uf+ Kf
⇒ Ui- Uf= Kf - Ki
⇒ Loss in Potential Energy = Gain in Kinetic Energy
⇒ Gain in Kinetic Energy = m.g. l .cos 30° = √3mgl/2
For a body of mass 1 kg U-x graph is shown in If the body is released from rest at x = 2m, then its speed when it crosses x = 5m is
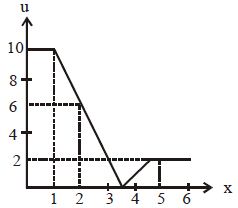
From Principal of Conservation of Energy
Ui + Ki = Uf + Kf
10 +0 = 2 + ½v²
⇒ v ² = 16 ⇒ v = 4 m/s
For a spring force-compression graph is shown in figure. A body of mass 5 kg moving with a speed of 8 ms–1 collides the The maximum compression in the spring is
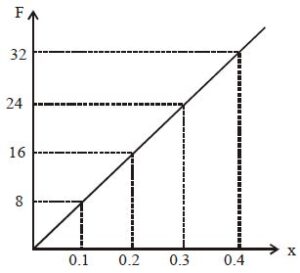

Using this graph we can find value of Spring constant.
F = - K.x
So, K = 80 N/m
Kinetic Energy of the block will convert into spring potential energy
so, ½mv² = ½ k x²
solving x = 2 m
A body of mass 2 kg collides with a massless spring of force constant K = 4 N/m. The spring compresses by 1m. If coefficient of friction between the body and the surface is 0.1, the speed of the body at the time of collision is :
The Kinetic Energy of the object will go to increase potential energy of the spring and a part of energy will be lost to friction
U1= ½ K x²= ½ × 4× 1² = 2J
Work done against friction = ü.mg.x= 0.1× 20 × 1= 2 J
So total kinetic energy is 4 = ½× 2 ×v ² ⇒ v = 2 m/s
The potential energy of a particle varies with distance x as shown in the graph :
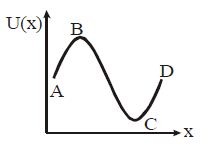
The force acting on the particle is zero at
For Equilibrium dU/dx =0 so, Points of maxima and minima in U-x graph are point of equilibrium.
So, Points B and C are equilibrium positions
A system absorbs 600 J of the system works equivalent to –900 J by The value of ΔE for the system is :
Work done by external agent = -900 J and energy supplied is 600 J So, change in kinetic energy is -300 J