An engine pumps 400 kg of water through height of 10 m in 40 s. Find the power of the pump (g = 10 m/s²).
Power = Work Done / Time Taken
Here , Work Done = 400 ×10 ×10 J = 40000 J
Time Taken = 40 sec , So,
Power = 40000/40 = 1000 W= 1 KW
An engine pumps 400 kg of water through height of 10 m in 40 s. Find the power of the engine if its efficiency is 80% (g = 10 m/s²).
Power = Work Done / Time Taken
Here , Work Done = 400 ×10 ×10 J = 40000 J
Time Taken = 40 sec , So,
Power = 40000/40 = 1000 W= 1 KW
Efficiency = Output Power/ Input Power × 100
⇒ 80 = 1000/ Input Power × 100
⇒Input Power = 1250 W= 1.25 KW
A force F = (iˆ + ˆj + 2kˆ) N is acting on a particle moving with constant velocity v = (iˆ + ˆj + kˆ) m/s. Power delivered by force is
Power is dot product of Force and Velocity
P = F.v
⇒ P= (iˆ + ˆj + 2kˆ). (iˆ + ˆj + kˆ)= 1+1+2= 4 watt
A block of mass 4 kg is pulled along a smooth inclined plane of inclination 30° with constant velocity 3 m/s as shown, power delivered by the force is
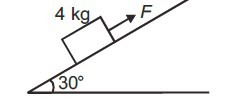
As the object is not moving with constant speed net force on it is zero.
so F = mg sin 30 °= 4 × 10 × ½= 20 N
Power is Dot product of force and velocity. So, P = 20 × 3 = 60 W
Water from a stream is falling on the blades of a turbine at the rate of 100 kg/s. If the height of the stream is 100 m, then power delivered to turbine is
Power is Rate of doing work.
Power = mgh/t= (m/t)gh= 100 × 10 × 100 = 100 kW
A body is being moved from rest along a straight line by a machine delivering constant power. The speed of body in time t is proportional to
Power = Constant (K)
F.v= K
⇒m.(dv/dt).v = K
⇒m.v.dv = K.dt
Integrating we get,
⇒∫m.v.dv=∫K.dt
⇒ mv²/2 = Kt
so, V α t½
A pump motor is used to deliver water at a certain rate from a given pipe. To obtain “2” time water from the same pipe in the same time, the amount to which the power of the motor should be increased is :
Force on water coming out is F= ρAv² and Power P=F.v
So, Power = F.v= ρAv³,
if v becomes 2v, Power P1= 8P