← Back to Work Energy and Power

Kinetic Energy and Momentum

Question 1:
A 1 kg mass has a kinetic energy of 1 joule when its speed is :

0.45 m/s

1 m/s

1.4 m/s

4.4 m/s

View Solution

Solution:

Kinetic Energy K = ½mv²

So, 1J = ½(1)v² so, v= √2 m/s= 1.414 m/s

Discuss this question

Question 2:
When the velocity of a body is doubled :

its kinetic energy is doubled

its potential energy is doubled

its acceleration is doubled

its momentum is doubled

View Solution

Solution:

Momentum of an object is P = m.v

So, when velocity is doubled momentum also doubles

Discuss this question

Question 3:
Two masses of 1 g and 4 g are moving with equal kinetic energies. The ratio of the magnitudes of their linear momenta is

1:2

√2:1

4:1

1:16

View Solution

Solution:

Kinetic Energy is given by K = ½mv² and Momentum is P=m.v, relation between kinetic energy and momentum is

K= P²/2m so P=√(2mK)

So P1/P2= √(m1)/√(m2)= √1/√4 = 1:2

Discuss this question

Question 4:
If the kinetic energy of a body is increased by 300%, its momentum will increase by :

100%

150%

200%

400%

View Solution

Solution:

Relation between Kinetic Energy and Momentum is

P = √(2mK)

When kinetic energy is increased by 300 % it becomes 4K so new momentum is

P1= √(2m.4K) =2P

Discuss this question

Question 5:
If the kinetic energy of a body is increased by 3%, its momentum will increase by :

1 %

1.5 %

3 %

4.5 %

View Solution

Solution:

K = P²/2m so,

∇K/K=2∇P/P

Solving We get , ∇P/P = 1.5%

Discuss this question

Question 6:
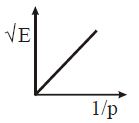
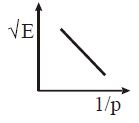
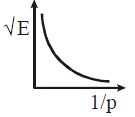
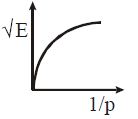
The graph between √E and 1/p is (E = kinetic energy and p = momentum):

View Solution

Solution:

Discuss this question