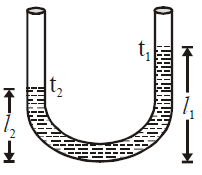
Question 5: Two rods, one of aluminium and the other made of steel, having initial length l1 and l2 are connected together to form a single rod of length (l1+ l2). The coefficients of linear expansion for aluminium and steel are αa and αs respectively. If the length of each rod increases by the same amount when their temperatures are raised by t°C, then find the ratio l1/(l1+ l2)
\[ \frac{\alpha_{s}}{\alpha_{a}} \]
\[ \frac{\alpha_{a}}{\alpha_{s}}\]
\[ \frac{\alpha_{s}}{\alpha_{a}+\alpha_{s}}\]
\[ \frac{\alpha_{a}}{\left( \alpha_{a}+\alpha_{s} \right)}\]
View Solution
Solution:
For the two rods to expand by the same length, their expansions \(\Delta l_1\) and \(\Delta l_2\) should be equal. The linear expansion for each rod can be written as:
\[
\Delta l_1 = l_1 \alpha_a t \quad \text{and} \quad \Delta l_2 = l_2 \alpha_s t
\]
Since \(\Delta l_1 = \Delta l_2\), we get:
\[
l_1 \alpha_a t = l_2 \alpha_s t
\]
Dividing both sides by \(t\) (assuming \(t \neq 0\)):
\[
l_1 \alpha_a = l_2 \alpha_s
\]
Now, to find the ratio \(\frac{l_1}{l_1 + l_2}\), divide both sides by \(\alpha_a + \alpha_s\):
\[
\frac{l_1}{l_1 + l_2} = \frac{\alpha_s}{\alpha_a + \alpha_s}
\]
So, the required ratio is:
\[
\frac{l_1}{l_1 + l_2} = \frac{\alpha_s}{\alpha_a + \alpha_s}
\]
Discuss this question