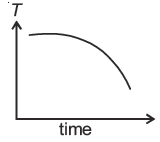
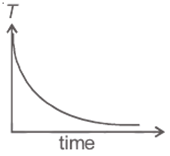
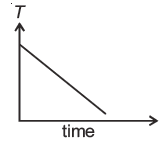
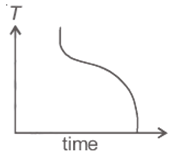
Question 5: A block of metal is heated to a temperature much higher than the room temperature and allowed to cool in a room free from air currents. Which of the following curves correctly represents the cooling? (T : Temperature of block)
View Solution
Solution:
To derive the exponential equation for Newton's law of cooling, we start with the differential form of Newton's law:
\[
\frac{dT}{dt} = -k (T - T_s)
\]
where:
- \( T \) is the temperature of the object at time \( t \),
- \( T_s \) is the temperature of the surroundings (constant),
- \( k \) is a positive constant of proportionality.
Step 1: Separate Variables
We can rewrite the equation as:
\[
\frac{dT}{T - T_s} = -k \, dt
\]
Step 2: Integrate Both Sides
Integrate both sides with respect to \( T \) and \( t \):
\[
\int \frac{1}{T - T_s} \, dT = -\int k \, dt
\]
This gives:
\[
\ln |T - T_s| = -kt + C
\]
where \( C \) is the integration constant.
Step 3: Exponentiate Both Sides
Exponentiate both sides to remove the logarithm:
\[
T - T_s = e^{-kt + C} = Ce^{-kt}
\]
where \( C = e^C \) is a new constant.
Step 4: Apply Initial Condition
Let \( T(0) = T_0 \), where \( T_0 \) is the initial temperature of the object. Then:
\[
T_0 - T_s = Ce^0 = C
\]
Thus, \( C = T_0 - T_s \), and the solution becomes:
\[
T = T_s + (T_0 - T_s)e^{-kt}
\]
Final Equation
\[
T(t) = T_s + (T_0 - T_s)e^{-kt}
\]
This is the exponential cooling equation that describes the temperature \( T \) of the object over time according to Newton's law of cooling. So the graph is exponentially decreasing function

Discuss this question