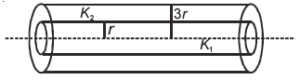
Solution:

The system shows two coaxial cylinders made of materials with different thermal conductivities (\(K_1\) and \(K_2\)) and radii \(r\) and \(3r\). For axial heat flow, the conductivities act in parallel.

To find the equivalent thermal conductivity (\(K_{\text{eq}}\)) of the entire system, we use the formula for thermal conductivities in parallel, similar to how resistances in parallel are treated for electrical systems:

\[
K_{\text{eq}} = \frac{K_1 A_1 + K_2 A_2}{A_1 + A_2}
\]

Where:
- \(A_1 = \pi r^2\) is the area of the inner cylinder.
- \(A_2 = \pi (3r)^2 - \pi r^2\  = 8\pi r^2\) is the area of the outer cylinder.

Substituting into the equation:

\[
K_{\text{eq}} = \frac{K_1 (\pi r^2) + K_2 (8\pi r^2)}{\pi r^2 + 8\pi r^2}
\]

Simplifying:

\[
K_{\text{eq}} = \frac{K_1 + 8K_2}{1 + 8} = \frac{K_1 + 8K_2}{9}
\]

Thus, the equivalent thermal conductivity is:

\[
K_{\text{eq}} = \frac{K_1 + 8K_2}{9}
\]

Discuss this question

Solution:

In heat transfer, natural convection is the method that is based on gravity.

Explanation:

Natural convection occurs due to the **buoyancy forces** that arise because of differences in fluid density caused by temperature gradients. When a fluid (like air or water) is heated, its density decreases, and it becomes lighter. The warmer, less dense fluid rises, and the cooler, denser fluid sinks under the influence of **gravity**. This creates a circulation pattern known as convection currents.

Thus, gravity is essential for this process, as it causes the movement of the fluid based on density differences. Without gravity, natural convection wouldn’t occur because there would be no buoyancy forces to drive the fluid motion.

Discuss this question

Solution:

The process in which the rate of heat transfer is maximum is radiation.

Explanation:

Radiation is the transfer of heat through electromagnetic waves (infrared radiation), which does not require any medium (solid, liquid, or gas) to propagate. This means that heat can be transferred even through a vacuum (like the heat from the Sun reaching the Earth).

Radiation is capable of transferring heat at the speed of light, making it a very efficient method of heat transfer. The rate of heat transfer by radiation depends on several factors:
- Temperature: The higher the temperature of the emitting body, the more heat it radiates.
- Surface properties: Objects with dark and rough surfaces radiate more heat than shiny or reflective ones (as described by the **Stefan-Boltzmann Law**).
- Emissivity: The efficiency of a material in emitting radiation.

In comparison to conduction (which requires a medium and is slower) and **convection** (which involves the motion of fluid and also depends on the medium), radiation can occur at a much faster rate, especially over long distances and in a vacuum. Thus, the rate of heat transfer by radiation can be the maximum, depending on the context and conditions.

Discuss this question

Solution:

The statement "Good absorbers of heat are good emitters" is explained by Kirchhoff's Law of Thermal Radiation.

Explanation:

Kirchhoff's law states that, for a body in thermal equilibrium, the ability to absorb radiation (absorptivity) is equal to its ability to emit radiation (emissivity) at the same temperature and wavelength. In simpler terms, materials that are good at absorbing heat also radiate or emit heat efficiently.

- Good absorbers: A material that can absorb a large amount of radiation from its surroundings is considered a good absorber. For example, objects with **dark, rough surfaces** absorb more heat than those with light, shiny surfaces.

- Good emitters: The same objects that absorb heat well also tend to emit heat efficiently when they are at a higher temperature than their surroundings. This is why a dark object, after absorbing heat, cools down faster by emitting more radiation compared to a shiny object.

For example:
- A black object absorbs more heat from sunlight (good absorber) and, when placed in the shade, radiates heat more quickly (good emitter).

Practical Example:

A black pot heats up quickly in the sun (good absorber) and cools down quickly at night (good emitter). Conversely, a shiny or reflective surface absorbs less heat and also emits less heat, meaning it retains heat longer.

This relationship between absorption and emission helps in designing materials for applications like thermal insulation, radiators, and solar panels.

Discuss this question

Solution:

A body that emits radiation at all possible wavelengths and absorbs all incident radiation, regardless of the wavelength or direction, is known as a perfect blackbody.

Explanation:

A perfect blackbody is an idealized object in thermodynamics and physics that has the following properties:

1. Perfect Absorber: It absorbs all radiation that falls on it, meaning it doesn't reflect or transmit any radiation. This is why it appears perfectly black.
2. Perfect Emitter: A blackbody is also the most efficient emitter of thermal radiation. At any given temperature, it emits the maximum amount of energy possible for that temperature across all wavelengths.

The radiation emitted by a blackbody is described by Planck's law and is dependent only on the body's temperature. The distribution of wavelengths emitted by a blackbody follows a characteristic curve, with the peak wavelength shifting according to Wien's displacement law as the temperature changes. The total energy emitted by the blackbody is given by the Stefan-Boltzmann law.

Examples:

• A perfect blackbody doesn't exist in the real world, but certain objects can approximate blackbody behavior. For instance, a small hole in a cavity acts like a nearly perfect blackbody because any radiation entering the hole is unlikely to escape.
• The Sun is often approximated as a blackbody in physics, though it's not perfect, it emits a nearly continuous spectrum of light.

Thus, a perfect blackbody is an ideal concept used to study and understand radiation emission and absorption.

Discuss this question

Solution:

In vacuum, the decrease in temperature of the hot body occurs due to radiation.

Explanation:

Since conduction and convection require a medium, they cannot occur in a vacuum. The only way heat can be transferred in a vacuum is through radiation, where the hot body emits electromagnetic waves (infrared radiation). This emission of radiation causes the temperature of the hot body to decrease over time, as it loses energy.

Discuss this question

Solution:

To find the equivalent thermal conductivity (\(K_{\text{eq}}\)) of the compound slab with two materials in series, we use the formula for thermal resistances in series.

Formula:
The total thermal resistance \(R_{\text{total}}\) for two materials in series is:

\[
R_{\text{total}} = R_1 + R_2 = \frac{L_1}{K_1 A} + \frac{L_2}{K_2 A}
\]

Where \(L_1 = L_2\) (equal thickness) and \(A\) is the cross-sectional area (same for both). The equivalent conductivity \(K_{\text{eq}}\) is given by:

\[
R_{\text{total}} = \frac{2L}{K_{\text{eq}} A}
\]

Given:
- Thickness of each layer, \(L_1 = L_2 = L/2\)
- Thermal conductivities \(K_1 = K\) and \(K_2 = 2K\)

Substitute into the resistance formula:

\[
R_{\text{total}} = \frac{L/2}{K A} + \frac{L/2}{2K A} = \frac{L}{2KA} + \frac{L}{4KA} = \frac{3L}{4KA}
\]

Now, equate this to the total resistance for the equivalent conductivity:

\[
\frac{2L}{K_{\text{eq}} A} = \frac{3L}{4KA}
\]

Solving for \(K_{\text{eq}}\):

\[
K_{\text{eq}} = \frac{4K}{3}
\]

Thus, the equivalent thermal conductivity of the slab is:

\[
K_{\text{eq}} = \frac{4K}{3}
\]

Discuss this question

Solution:

To find the temperature at the interface of the rectangular slab, we use the concept of  thermal conduction through two materials in series.

Given:
- Thermal conductivity of iron, \(K_{\text{iron}} = 0.2 \, \text{W/mK}\)
- Thermal conductivity of brass, \(K_{\text{brass}} = 0.3 \, \text{W/mK}\)
- Temperature at one side of the iron slab, \(T_{\text{iron}} = 100^\circ C\)
- Temperature at one side of the brass slab, \(T_{\text{brass}} = 0^\circ C\)
- Thicknesses of both slabs are equal.

Since the slabs are in series and have equal thicknesses, the **heat flux** through both materials is the same. Using the formula for heat conduction, the temperature at the interface \(T_{\text{interface}}\) can be calculated using the ratio of thermal conductivities:

\[
\frac{T_{\text{iron}} - T_{\text{interface}}}{T_{\text{interface}} - T_{\text{brass}}} = \frac{K_{\text{brass}}}{K_{\text{iron}}}
\]

Substitute the known values:

\[
\frac{100 - T_{\text{interface}}}{T_{\text{interface}} - 0} = \frac{0.3}{0.2} = 1.5
\]

Now solve for \(T_{\text{interface}}\):

\[
100 - T_{\text{interface}} = 1.5 T_{\text{interface}}
\]

\[
100 = 2.5 T_{\text{interface}}
\]

\[
T_{\text{interface}} = \frac{100}{2.5} = 40^\circ C
\]

Thus, the temperature at the interface is \(40^\circ C\).

Discuss this question

Solution:

In lakes, temperature stratification occurs, where different layers of water have distinct temperatures.

- Surface Temperature (2°C): The surface of the lake cools down and can freeze when temperatures drop, resulting in water that is less dense.

- Bottom Temperature (4°C): Water reaches its maximum density at 4°C. Below this temperature, water becomes less dense, causing it to rise. Therefore, in many lakes, the bottom water remains at around 4°C, even when the surface is colder.

This stratification helps maintain aquatic life during cold seasons, as the bottom layer remains relatively stable and can support organisms.

Discuss this question

Solution:

To find the temperature difference (ΔT) between the two ends of the conductor, we can use the formula for heat conduction:

\[
Q = \frac{K \cdot A \cdot \Delta T}{L}
\]

Where:
- \( Q = 6000 \, \text{J/s} \)
- \( K = 200 \, \text{J} \, \text{m}^{-1} \, \text{K}^{-1} \)
- \( A = 0.75 \, \text{m}^2 \)
- \( L = 1 \, \text{m} \)

Rearranging to solve for ΔT:

\[
\Delta T = \frac{Q \cdot L}{K \cdot A}
\]

\[
\Delta T = \frac{6000 \cdot 1}{200 \cdot 0.75} = 40 \, \text{K}
\]

The temperature difference between the two ends is 40 K or 40 °C

Discuss this question