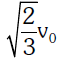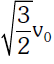Solution:

The total mechanical energy \( E \) of a satellite in a circular orbit is the sum of its kinetic energy \( K \) and potential energy \( U \).

1. **Kinetic Energy (K):**

\[
K = \frac{1}{2} m v^2
\]

2. **Potential Energy (U):**

\[
U = -\frac{GMm}{r}
\]

For a satellite orbiting closely around the Earth, its velocity \( v \) is related to the Earth's gravitational constant by:

\[
v = \sqrt{\frac{GM}{r}}
\]

Substitute \( v^2 = \frac{GM}{r} \) into the kinetic energy expression:

\[
K = \frac{1}{2} m \left( \frac{GM}{r} \right) = \frac{GMm}{2r}
\]

Now, the **total energy** is:

\[
E = K + U = \frac{GMm}{2r} - \frac{GMm}{r} = -\frac{GMm}{2r}
\]

Thus, the total energy of the satellite is:

\[
E = -\frac{GMm}{2r}= -\frac{1}{2}mv^{2}
\]

Discuss this question

Solution:

The orbital period of a satellite depends only on the radius of its orbit and the mass of the Earth, not on the mass of the satellite itself. The period \( T \) is given by:

\[
T = 2\pi \sqrt{\frac{r^3}{GM}}
\]

Since the masses of the satellites do not appear in this formula, the periods of the two satellites will be the same if they are in the same orbit, regardless of their masses.

Therefore, the ratio of their periods of revolution is:

\[
\frac{T_1}{T_2} = 1
\]

So, the ratio is 1:1.

Discuss this question

Solution:

If the Earth's radius shrinks to half, but its mass remains the same, the orbital period of the satellite will not change.

The orbital period \( T \) of a satellite depends on the mass of the Earth \( M \) and the radius of the orbit \( r \), not the radius of the Earth itself. The formula for the period of a satellite in orbit is:

\[
T = 2\pi \sqrt{\frac{r^3}{GM}}
\]

Since the mass \( M \) of the Earth and the radius \( r \) of the satellite’s orbit (which is unaffected by the Earth shrinking) remain the same, the period \( T \) remains unchanged.

Thus, the new period of revolution will still be \( T \).

Discuss this question

Solution:

The energy required to move a satellite from one orbit to another can be found using the difference in total mechanical energy between the two orbits.

The total energy \( E \) of a satellite in orbit of radius \( r \) is:

\[
E = -\frac{GMm}{2r}
\]

For the initial orbit of radius \( r \), the energy is:

\[
E_1 = -\frac{GMm}{2r}
\]

For the final orbit of radius \( \frac{3r}{2} \), the energy is:

\[
E_2 = -\frac{GMm}{2 \times \frac{3r}{2}} = -\frac{GMm}{3r}
\]

The energy required to shift the satellite is the difference between the two energies:

\[
\Delta E = E_2 - E_1 = \left(-\frac{GMm}{3r}\right) - \left(-\frac{GMm}{2r}\right)
\]

\[
\Delta E = \frac{GMm}{2r} - \frac{GMm}{3r} = \frac{GMm}{6r}
\]

So, the energy required is:

\[
\Delta E = \frac{GMm}{6r}
\]

Discuss this question

Solution:

The orbital velocity \( v \) at a height \( h \) above the Earth's surface is given by:

\[
v = \sqrt{\frac{GM}{R + h}}
\]

For the satellite orbiting just above the Earth's surface (i.e., \( h = 0 \)), the velocity is:

\[
v_0 = \sqrt{\frac{GM}{R}}
\]

For a satellite at an altitude of \( h = \frac{R}{2} \), the velocity \( v_h \) becomes:

\[
v_h = \sqrt{\frac{GM}{R + \frac{R}{2}}} = \sqrt{\frac{GM}{\frac{3R}{2}}} = \sqrt{\frac{2}{3}} v_0
\]

Thus, the orbital velocity at an altitude of \( \frac{R}{2} \) is:

\[
v_h = \sqrt{\frac{2}{3}} v_0
\]

Discuss this question

Solution:

The orbital speed \( v \) of a satellite is given by:

\[
v = \sqrt{\frac{GM}{r}}
\]

where \( r \) is the radius of the orbit.

Let the speeds of satellites A and B be \( v_A \) and \( v_B \), and their orbital radii be \( 4R \) and \( R \), respectively. Using the relation:

\[
v_A = \sqrt{\frac{GM}{4R}}, \quad v_B = \sqrt{\frac{GM}{R}}
\]

Given \( v_A = 3v \), we can write:

\[
3v = \sqrt{\frac{GM}{4R}}
\]

Now, the speed of satellite B is:

\[
v_B = \sqrt{\frac{GM}{R}} = 2 \times \sqrt{\frac{GM}{4R}} = 2 \times 3v = 6v
\]

So, the speed of satellite B is \( 6v \).

Discuss this question

Solution:

The orbital speed \( v \) of a satellite is given by:

\[
v = \sqrt{\frac{GM}{R}}
\]

where \( R \) is the distance from the center of the Earth to the satellite and \( g \) is the acceleration due to gravity at the Earth's surface. Using the relation \( g = \frac{GM}{R_e^2} \), where \( R_e \) is the Earth's radius, we can rewrite the formula as:

\[
v = \sqrt{g \cdot \frac{R_e^2}{R}}
\]

Here, \( R = R_e + h \), where \( h = 0.25 \times 10^6 \) m is the height above the surface of the Earth.

Now, substituting values:

\[
R = 6.38 \times 10^6 + 0.25 \times 10^6 = 6.63 \times 10^6 \, \text{m}
\]

\[
v = \sqrt{9.8 \times \frac{(6.38 \times 10^6)^2}{6.63 \times 10^6}}
\]

Solving:

\[
v \approx 7.76 \, \text{km/s}
\]

So, the orbital speed of the satellite is approximately \( 7.76 \, \text{km/s} \).

Discuss this question

Solution:

Yes, the acceleration of the satellite \( S \) is always directed towards the center of the Earth. This is because the gravitational force, which provides the acceleration, always points towards the Earth's center, regardless of the satellite's position in its elliptical orbit. This centripetal acceleration is responsible for keeping the satellite in orbit.

Discuss this question

Solution:

According to **Kepler's second law** (law of areas), a planet sweeps out equal areas in equal times. This means the area swept out is proportional to the time taken.

In the problem, the area \( SCD \) is given to be twice the area \( SAB \). Therefore, the time taken to sweep these areas will also follow the same ratio.

Thus, the relation between the times is:

\[
t_1 = 2 t_2
\]

So, the time taken to move from \( C \) to \( D \) is twice the time taken to move from \( A \) to \( B \).

Discuss this question

Solution:

For a planet in an elliptical orbit:

- Total energy (E) is the sum of kinetic energy (T) and potential energy (U).
- In a bound orbit like an ellipse, E is always negative. This indicates that the planet is gravitationally bound to the star and cannot escape.
- Kinetic energy (T) is always positive.
- Potential energy (U) is negative due to the attractive gravitational force, and its magnitude is greater than T.
- Angular momentum (L) is constant for elliptical orbits.

Thus, E is always negative for elliptical orbits.

Discuss this question