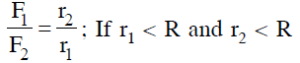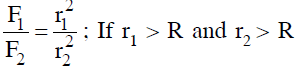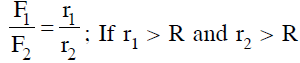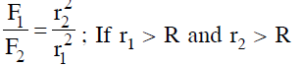Solution:

The gravitational force between two masses \( m_1 \) and \( m_2 \) is:

\[
F = G \frac{m_1 \cdot m_2}{r^2}
\]

To maximize \( F \), we set \( m_1 = x \) and \( m_2 = 100 - x \), then maximize the product \( m_1 \cdot m_2 = x(100 - x) \).

This product is maximized when \( x = 50 \). So, the masses should be split equally.

The ratio of masses is:

\[
\frac{m_1}{m_2} = \frac{50}{50} = 1
\]

Discuss this question

Solution:

According to Newton’s third law, for every action, there is an equal and opposite reaction. The Earth exerts a gravitational force on the Moon, and the Moon exerts an equal and opposite gravitational force on the Earth. This reaction force is the gravitational force on Earth by the Moon.

Discuss this question

Solution:

The initial gravitational force between two bodies is:

\[
F = G \frac{m \cdot m}{r^2}
\]

After transferring 25% of mass from one body to the other, the new masses become \( 0.75m \) and \( 1.25m \), and the separation becomes \( \frac{r}{2} \). The new gravitational force is:

\[
F' = G \frac{(0.75m)(1.25m)}{\left(\frac{r}{2}\right)^2}
\]

Simplifying:

\[
F' = G \frac{0.9375 m^2}{\frac{r^2}{4}} = 4 \times 0.9375 \times \frac{G m^2}{r^2} = 15F/4
\]

So, the new gravitational force is:

\[
F' = 3.75F= 15F/4
\]

Discuss this question

Solution:

If the universal constant of gravitation \( G \) were decreasing uniformly with time, the gravitational force between the satellite and the Earth would weaken. However, the satellite's angular momentum would remain conserved because angular momentum depends on the mass, velocity, and radius of orbit, and not directly on \( G \).

According to the law of conservation of angular momentum:

\[
L = m v r
\]

where \( L \) is angular momentum, \( m \) is the satellite's mass, \( v \) is its velocity, and \( r \) is the orbital radius. Since no external torque acts on the system, angular momentum is conserved even if \( G \) changes.

However, the satellite’s orbital parameters like its velocity and orbital radius might change over time due to the weakening gravitational force, but the total angular momentum will remain constant.

Discuss this question

Solution:

When both \( r_1 \) and \( r_2 \) are greater than \( R \) (i.e., both are outside the sphere), the gravitational force at a distance \( r \) from the center of a uniform sphere is given by:

\[
F = \frac{G M}{r^2}
\]

So, the forces \( F_1 \) and \( F_2 \) at distances \( r_1 \) and \( r_2 \) from the center are:

\[
F_1 = \frac{G M}{r_1^2}
\]
\[
F_2 = \frac{G M}{r_2^2}
\]

Now, taking the ratio \( \frac{F_1}{F_2} \):

\[
\frac{F_1}{F_2} = \frac{\frac{G M}{r_1^2}}{\frac{G M}{r_2^2}} = \frac{r_2^2}{r_1^2}
\]

Thus, the ratio of the gravitational forces is:

\[
\frac{F_1}{F_2} = \left( \frac{r_2}{r_1} \right)^2
\]

Discuss this question

Solution:

The weight of an object on the Moon is given by:

\[
W_{\text{moon}} = \frac{1}{6} W_{\text{earth}}
\]

Weight is related to the gravitational acceleration \( g \) by:

\[
W = mg
\]

Thus,

\[
g_{\text{moon}} = \frac{1}{6} g_{\text{earth}}
\]

The formula for gravitational acceleration is:

\[
g = \frac{GM}{R^2}
\]

Where:
- \( G \) is the gravitational constant,
- \( M \) is the mass of the Moon,
- \( R \) is the radius of the Moon.

Given:
- \( g_{\text{earth}} = 9.8 \, \text{m/s}^2 \),
- \( g_{\text{moon}} = \frac{1}{6} \times 9.8 = 1.633 \, \text{m/s}^2 \),
- \( R_{\text{moon}} = 1.768 \times 10^6 \, \text{m} \).

Now, solve for \( M_{\text{moon}} \) using:

\[
g_{\text{moon}} = \frac{G M_{\text{moon}}}{R_{\text{moon}}^2}
\]

Rearranging for \( M_{\text{moon}} \):

\[
M_{\text{moon}} = \frac{g_{\text{moon}} R_{\text{moon}}^2}{G}
\]

Substitute values:

\[
M_{\text{moon}} = \frac{1.633 \times (1.768 \times 10^6)^2}{6.674 \times 10^{-11}}
\]

Calculating this gives:

\[
M_{\text{moon}} \approx 7.35 \times 10^{22} \, \text{kg}
\]

Thus, the mass of the Moon is approximately \( 7.35 \times 10^{22} \, \text{kg} \).

Discuss this question

Solution:

The gravitational force between two masses \( m_1 \) and \( m_2 \) is given by Newton's law of gravitation:

\[
F = \frac{G m_1 m_2}{r^2}
\]

Let the total mass be \( M = 100 \, \text{kg} \), and split it into two parts: \( m_1 = x \) and \( m_2 = 100 - x \).

The gravitational force becomes:

\[
F = \frac{G x (100 - x)}{r^2}
\]

To maximize \( F \), we need to maximize \( x(100 - x) \), which is a quadratic function. The product \( x(100 - x) \) is maximized when \( x = 50 \).

Thus, the ratio of the two masses is:

\[
m_1 : m_2 = 50 : 50 = 1:1
\]

Therefore, the masses should be in a 1:1 ratio for the gravitational force to be maximum.

Discuss this question

Solution:

The formula for acceleration due to gravity \( g \) on a planet is:

\[
g = \frac{GM}{R^2}
\]

Where:
- \( G \) is the gravitational constant,
- \( M \) is the mass of the planet,
- \( R \) is the radius of the planet.

Mass \( M \) is related to density \( \rho \) and volume \( V \):

\[
M = \rho V = \rho \frac{4}{3} \pi R^3
\]

Substituting into the equation for \( g \):

\[
g = \frac{G \rho \frac{4}{3} \pi R^3}{R^2} = \frac{4}{3} \pi G \rho R
\]

Thus, \( g \propto \rho R \).

Given:
- Diameter ratio \( R_1 : R_2 = 4:1 \), so \( R_1 : R_2 = 4:1 \),
- Density ratio \( \rho_1 : \rho_2 = 1:2 \).

Now,

\[
g_1 : g_2 = (\rho_1 R_1) : (\rho_2 R_2) = (1 \times 4) : (2 \times 1) = 4:2 = 2:1
\]

Thus, the ratio of acceleration due to gravity on the planets is \( 2:1 \).

Discuss this question

Solution:

To find the dimensions of the gravitational constant \( G \), use Newton's law of gravitation:

\[
F = \frac{G M_1 M_2}{r^2}
\]

Where:
- \( F \) is force (with dimensions \( [M L T^{-2}] \)),
- \( M_1 \) and \( M_2 \) are masses (with dimensions \( [M] \)),
- \( r \) is distance (with dimensions \( [L] \)).

Rearranging for \( G \):

\[
G = \frac{F r^2}{M_1 M_2}
\]

Substitute the dimensions:

\[
G = \frac{[M L T^{-2}] [L^2]}{[M][M]}
\]

Simplify:

\[
G = [M^{-1} L^3 T^{-2}]
\]

Thus, the dimensions of \( G \) are \( [M^{-1} L^3 T^{-2}] \).

Discuss this question