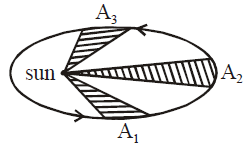
A planet moving around sun sweeps area A1 in 2 days, A2 in 3 days and A3 in 6 days. Then the relation between A1, A2 and A3 is :
Solution:
According to **Kepler's Second Law** (the Law of Equal Areas), a line segment joining a planet and the Sun sweeps out equal areas in equal times. Therefore, the area swept out in a given time is proportional to the time interval.
### Given:
- Area \( A_1 \) is swept in 2 days.
- Area \( A_2 \) is swept in 3 days.
- Area \( A_3 \) is swept in 6 days.
### Area Swept Proportions:
Since the area swept is proportional to the time taken:
\[
\frac{A_1}{A_2} = \frac{2 \text{ days}}{3 \text{ days}} \quad \Rightarrow \quad A_1 = \frac{2}{3} A_2
\]
\[
\frac{A_2}{A_3} = \frac{3 \text{ days}}{6 \text{ days}} \quad \Rightarrow \quad A_2 = \frac{1}{2} A_3
\]
### Relating Areas:
Substituting the relationship of \( A_2 \) in \( A_1 \):
\[
A_1 = \frac{2}{3} \left(\frac{1}{2} A_3\right) = \frac{1}{3} A_3
\]
### Final Relationships:
Now, we can express the areas in terms of \( A_3 \):
- \( A_1 = \frac{1}{3} A_3 \)
- \( A_2 = \frac{1}{2} A_3 \)
### Conclusion:
The relationship between the areas \( A_1 \), \( A_2 \), and \( A_3 \) can be summarized as:
\[
A_1 : A_2 : A_3 = 1 : \frac{3}{2} : 3
\]
This can also be expressed as:
\[
A_1 : A_2 : A_3 = 2: 3 : 6
\]