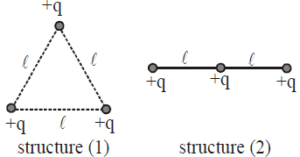
Three charges –q, +Q and –q are placed in a straight line as shown.
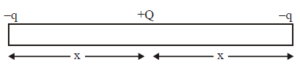
If the total potential energy of the system is zero, then the ratio q/Q is
Solution:
To find the ratio \( q/Q \), we need to calculate the total potential energy of the system and set it to zero. The charges are arranged in a straight line as shown:
Charges:
1. \( -q \) at one end.
2. \( +Q \) in the middle.
3. \( -q \) at the other end.
Distances:
- Distance between \( -q \) and \( +Q \): \( x \).
- Distance between \( +Q \) and the other \( -q \): \( x \).
- Total distance between the two \( -q \) charges: \( 2x \).
Potential Energy of the System:
The potential energy \( U \) for each pair of charges is given by:
\[
U = \frac{kq_1q_2}{r},
\]
where \( q_1 \) and \( q_2 \) are the charges, \( r \) is the distance between them, and \( k \) is Coulomb's constant.
1. Interaction between \( -q \) and \( +Q \) (on one side):
\[
U_1 = \frac{k(-q)(+Q)}{x} = -\frac{kqQ}{x}.
\]
2. Interaction between \( +Q \) and \( -q \) (on the other side):
\[
U_2 = \frac{k(+Q)(-q)}{x} = -\frac{kqQ}{x}.
\]
3. Interaction between \( -q \) and \( -q \) (across the distance \( 2x \)):
\[
U_3 = \frac{k(-q)(-q)}{2x} = \frac{kq^2}{2x}.
\]
Total Potential Energy:
\[
U_{\text{total}} = U_1 + U_2 + U_3 = -\frac{kqQ}{x} - \frac{kqQ}{x} + \frac{kq^2}{2x}.
\]
Simplify:
\[
U_{\text{total}} = -\frac{2kqQ}{x} + \frac{kq^2}{2x}.
\]
Set \( U_{\text{total}} = 0 \):
\[
-\frac{2kqQ}{x} + \frac{kq^2}{2x} = 0.
\]
Factor out \( \frac{k}{x} \):
\[
-\frac{2qQ}{1} + \frac{q^2}{2} = 0.
\]
Multiply through by 2 to eliminate the fraction:
\[
-4qQ + q^2 = 0.
\]
Factorize:
\[
q(q - 4Q) = 0.
\]
Since \( q \neq 0 \), we have:
\[
q = 4Q.
\]
Ratio:
\[
\frac{q}{Q} = 4.
\]