← Back to Electrostatics

Electric Field

Question 1:
As shown in the diagram, two fixed charges, q1 = +1.00 μC and q2 = –4.00 μC, are 0.200 m apart. Where is the total field zero?

0.40 m to the right of q1

0.13 m to the right of q1

0.20 m to the left of q1

0.067 m to the left of q1

View Solution

No solution provided for this question.

Question 2:
Four charges are placed on the circumference of a circle of radius R, 90° apart as shown in the fig.The electric field strength at the centrer of the circle is

\frac{1}{4\pi\varepsilon_{0}}\frac{2\sqrt{5}Q}{R^{2}}, making angle tan^{-1}2 with the -ve axis

\frac{1}{4\pi\varepsilon_{0}}\frac{2\sqrt{5}Q}{R^{2}}, making angle tan^{-1}2 with the +ve axis

\frac{1}{4\pi\varepsilon_{0}}\frac{4\sqrt{2}Q}{R^{2}}, making angle tan^{-1}\frac{1}{2} with the -ve axis

\frac{1}{4\pi\varepsilon_{0}}\frac{4\sqrt{2}Q}{R^{2}}, making angle tan^{-1}\frac{1}{2} with the +ve axis

View Solution

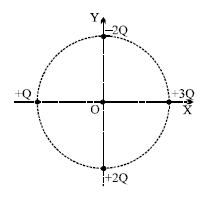
No solution provided for this question.

Question 3:
The charge per unit length of the four quadrant of the ring is 2λ , – 2λ , λ and -λ respectively. Th e electric field at the centre is

-\frac{\lambda}{2\pi\varepsilon_{0}R}\hat{i}

\frac{\lambda}{2\pi\varepsilon_{0}R}\hat{j}

\frac{\sqrt{2}\lambda}{4\pi\varepsilon_{0}R}\hat{i}

None

View Solution

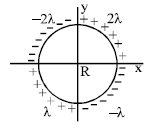
No solution provided for this question.

Question 4:
A thin semi-circular ring of radius r has a positive charge q distributed uniformly over it. The net field \overrightarrow{E} at the centre O is :

-\frac{q}{2\pi^{2}\varepsilon_{0}r^{2}}\hat{j}

\frac{q}{2\pi^{2}\varepsilon_{0}r^{2}}\hat{j}

\frac{q}{4\pi^{2}\varepsilon_{0}r^{2}}\hat{j}

-\frac{q}{4\pi^{2}\varepsilon_{0}r^{2}}\hat{j}

View Solution

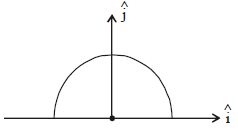
No solution provided for this question.

Question 5:
In the figure , ΔABC is in an isosceles triangle with A = 90°. D is the mid point of BC. Three charges 2Q, –Q and Q are placed at A, B, C respectively.
The net electric field at D due to three charges is directed along the numbered arrow :

View Solution

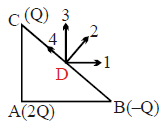
No solution provided for this question.

Question 6:
Find the electric field due to a circular arc of radius R and charge / length l at the origin. The arc is in xy plane and extends from θ = π/3 to θ = p w .r.t.
x-axis .

\frac{\sqrt{3}k\lambda}{R}\left[ cos30^{0}\hat{i}-sin30^{0}\hat{j} \right]

\frac{\sqrt{3}k\lambda}{R}\left[ cos60^{0}\hat{i}-sin60^{0}\hat{j} \right]

\frac{k\lambda}{2R}\left[ cos30^{0}\hat{i}-sin30^{0}\hat{j} \right]

\frac{k\lambda}{2R}\left[ cos60^{0}\hat{i}-sin60^{0}\hat{j} \right]

View Solution

No solution provided for this question.

Question 7:
A block of mass m containing a net negative charge –q is placed on a frictionless horizontal table and is connected to a wall through an
unstretched spring of spring constant k. If the horizontal electric field E parallel to the spring is switched on, then the maximum compression
of the spring is :-

\sqrt{qE/k}

2qE/k

qE/k

zero

View Solution

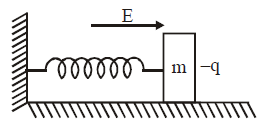
No solution provided for this question.

Question 8:
A point charge of 100 μC is placed at 3\hat{i}+4\hat{j} m. Find the electric field intensity due to this charge at a point located at 9\hat{i}+12\hat{j} m :-

8000 Vm^{-1}

9000 Vm^{-1}

2250 Vm^{-1}

4500 Vm^{-1}

View Solution

No solution provided for this question.

Question 9:
Five point charges, each of value +q, are placed on five vertices of a regular hexagon of side L. The magnitude of the force on a point charge of value –q coulomb placed at the center of the hexagon is

\frac{1}{\pi\varepsilon_{0}}\left( \frac{q}{L} \right)^{2}

\frac{2}{\pi\varepsilon_{0}}\left( \frac{q}{L} \right)^{2}

\frac{1}{2\pi\varepsilon_{0}}\left( \frac{q}{L} \right)^{2}

\frac{1}{4\pi\varepsilon_{0}}\left( \frac{q}{L} \right)^{2}

View Solution

No solution provided for this question.

Question 10:
A thin glass rod is bent into a semicircle of radius r. A charge +Q is uniformly
distributed along the upper half, and a charge –Q is uniformly distributed along the lower half, as shown in Fig. The electric field E at P, the center of the semicircle, is :

\[ \frac{Q}{\pi^{2}\varepsilon_{0}r^{2}}\]

\[ \frac{2Q}{\pi^{2}\varepsilon_{0}r^{2}}\]

\[ \frac{4Q}{\pi^{2}\varepsilon_{0}r^{2}}\]

\[ \frac{Q}{4\pi^{2}\varepsilon_{0}r^{2}}\]

View Solution

Solution:

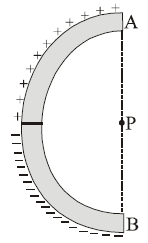
Using the direct formula for the electric field due to a uniformly charged arc:

\[
E = \frac{2k\lambda \sin(\theta/2)}{r}
\]

Step 1: Identify Parameters
- \(\lambda\): Linear charge density.
- \(k = \frac{1}{4 \pi \varepsilon_0}\): Coulomb's constant.
- \(r\): Radius of the semicircle.
- \(\theta = \pi\): Angle subtended by the semicircle at the center.

Step 2: Substitute \(\lambda\)
The total charge on the semicircle is \(+Q\) or \(-Q\), and the arc length is \(\pi r\). Therefore:
\[
\lambda = \frac{Q}{\pi r}
\]

Step 3: Substitute into the Formula
\[
E = \frac{2k \lambda \sin(\pi/2)}{r}
\]
Here, \(\sin(\pi/2) = 1\). Substituting \(\lambda = \frac{Q}{\pi r}\):
\[
E = \frac{2k \left(\frac{Q}{\pi r}\right)}{r}
\]

Step 4: Simplify
\[
E = \frac{2k Q}{\pi r^2}
\]

Since \(k = \frac{1}{4 \pi \varepsilon_0}\), substitute \(k\):
\[
E = \frac{2}{4 \pi \varepsilon_0} \cdot \frac{Q}{\pi r^2}
\]

\[
E = \frac{Q}{\pi^2 \varepsilon_0 r^2}
\]

Final Answer:
The electric field at the center is:
\[
{\frac{Q}{\pi^2 \varepsilon_0 r^2}}
\]

Discuss this question

1 2 Next »