← Back to Electrostatics

Electric Dipole

Question 1:
An electric dipole of moment ‘p’ is placed in an electric field of intensity ‘E’. The dipole acquires a position such that the axis of the dipole makes an angle θ with the direction of the field. Assuming that the potential energy of the dipole to be zero when θ = 90°. the torque and the potential energy of the dipole will respectively be :

pE sin θ, 2pE cos θ

pE cos θ, – pE sin θ

pE sin θ, –pE cos θ

pE sin θ, –2pE cos θ

View Solution

Solution:

The torque acting on the dipole in an electric field is given by:

\[
\tau = pE \sin\theta
\]

The potential energy of the dipole is defined as:

\[
U = -pE \cos\theta
\]

Here, the potential energy is zero when \( \theta = 90^\circ \), which aligns with the condition provided.

Discuss this question

Question 2:
An electric dipole with dipole moment

\( \overrightarrow{p}=\left( 3\hat{i}+4\hat{j} \right) \) C-m, is kept in electric field \(\overrightarrow{E}=0.4kN/C\hat{i} \). What is the torque acting on it & the potential energy of the dipole ?

\[ 1600\left( N\times m \right)\hat{k},-1200J\]

\[ -1600\left( N\times m \right)\hat{k},1200J\]

\[ -1600\left( N\times m \right)\hat{k},-1200J \]

\[ 1600\left( N\times m \right)\hat{k},1200J \]

View Solution

Solution:

Given:
- Dipole moment: \( \overrightarrow{p} = 3\hat{i} + 4\hat{j} \) C·m
- Electric field: \( \overrightarrow{E} = 0.4 \, \text{kN/C} \hat{i} = 400 \, \text{N/C} \hat{i} \)

Torque (\( \overrightarrow{\tau} \)):
\[
\overrightarrow{\tau} = \overrightarrow{p} \times \overrightarrow{E}
\]

\[
\overrightarrow{\tau} = \begin{vmatrix}
\hat{i} & \hat{j} & \hat{k} \\
3 & 4 & 0 \\
400 & 0 & 0
\end{vmatrix} = \hat{k} \big(3(0) - 4(400)\big) = -1600\hat{k} \, \text{N·m}
\]

Potential Energy (\( U \)):
\[
U = -\overrightarrow{p} \cdot \overrightarrow{E}
\]
\[
U = -(3 \times 400 + 4 \times 0) = -1200 \, \text{J}
\]

Final Answer:
- Torque: \( -1600 \, \text{N·m} \hat{k} \)
- Potential energy: \( -1200 \, \text{J} \)

Discuss this question

Question 3:
An electric dipole with dipole moment \( 2\times 10^{-9} \)Cm is aligned at 30º with the direction of a uniform electric field of magnitude \( 4\times 10^{4} NC^{-1}\). The magnitude of the torque acting on the dipole is :

\[ 2\times 10^{-5} Nm\]

\[ 2\times 10^{-4} Nm\]

\[ 4\times 10^{-4} Nm\]

\[ 4\times 10^{-5} Nm\]

View Solution

Solution:

Given:
- Dipole moment: \( p = 2 \times 10^{-9} \, \text{C·m} \)
- Electric field: \( E = 4 \times 10^{4} \, \text{N/C} \)
- Angle: \( \theta = 30^\circ \)

Torque (\( \tau \)):
\[
\tau = pE \sin\theta
\]
\[
\tau = (2 \times 10^{-9})(4 \times 10^{4}) \sin 30^\circ
\]
\[
\tau = (8 \times 10^{-5}) \times \frac{1}{2} = 4 \times 10^{-5} \, \text{N·m}
\]

Final Answer:
\[
\tau = 4 \times 10^{-5} \, \text{N·m}
\]

Discuss this question

Question 4:
A dipole of electric dipole moment p is placed in a uniform electric field of strength E. If θ is the angle between positive directions of p and E, then the potential energy of the electric dipole is largest when θ is :

π/4

π/2

Zero

View Solution

Solution:

The potential energy (\(U\)) of an electric dipole in a uniform electric field is given by:

\[
U = -\mathbf{p} \cdot \mathbf{E} = -pE \cos\theta
\]

Here:
- \(p\) is the magnitude of the dipole moment,
- \(E\) is the magnitude of the electric field,
- \(\theta\) is the angle between \(\mathbf{p}\) and \(\mathbf{E}\).

The potential energy is largest when \(-\cos\theta\) is most positive, i.e., when \(\cos\theta = -1\). This happens at:

\[
\theta = \pi \ (\text{180°})
\]

At this angle, the dipole is aligned opposite to the electric field, and the potential energy is \(U = +pE\), its maximum value.

Discuss this question

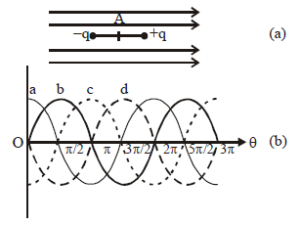
Question 5:
The electric dipole is situated in an electric field as shown in figure. The dipole and electric field are both in the plane of paper. The dipole is rotated about an axis perpendicular to the paper at point A in anticlockwise direction. If the angle of rotation is measured with respect to the direction of the electric field then the torque for different values of the angle of rotation θ will be as represented in figure :
[Take direction inside the paper as positive]

View Solution

Solution:

For an electric dipole in a uniform electric field, the torque \( \tau \) on the dipole is given by:

\[
\tau = pE \sin \theta
\]

where:
- \( p \) is the dipole moment,
- \( E \) is the electric field strength,
- \( \theta \) is the angle between the dipole and the electric field.

Analysis:

1. Torque Variation:
- The torque \( \tau \) is maximum when \( \theta = \frac{\pi}{2}, \frac{3\pi}{2}, \dots \) (odd multiples of \( \frac{\pi}{2} \)), as \( \sin \theta = \pm 1 \).
- The torque \( \tau \) is zero when \( \theta = 0, \pi, 2\pi, \dots \), as \( \sin \theta = 0 \).

2. Graph Interpretation:
- The correct graph of \( \tau \) versus \( \theta \) will have positive and negative peaks at \( \theta = \frac{\pi}{2}, \frac{3\pi}{2}, \dots \), and cross zero at \( \theta = 0, \pi, 2\pi, \dots \).

Conclusion:

The correct answer is (b) as it represents the sinusoidal variation of torque with respect to \( \theta \) with alternating positive and negative values, matching the behavior of \( \tau = pE \sin \theta \).

Discuss this question

Question 6:
A point Q lies on the perpendicular bisector of an electric dipole of dipole moment p. If the distance of Q from the dipole is r (much larger than the size of the dipole) then electric field at Q is proportional to :

\(p^{-1} \)and \( r^{-2}\)

p and \( r^{-2}\)

\(p^{2}\) and \(r^{-3}\)

p and \( r^{-3}\)

View Solution

Solution:

For a point \( Q \) on the perpendicular bisector of an electric dipole (distance \( r \) from the center, where \( r \gg \text{dipole length} \)):

1. Electric Field on Perpendicular Bisector: The electric field \( E \) at a point on the perpendicular bisector of a dipole is given by:
\[
E \propto \frac{p}{r^3}
\]

2. Dependence:
- Directly proportional to the dipole moment \( p \).
- Inversely proportional to \( r^3 \).

Answer:
The electric field at \( Q \) is proportional to:
\[
p \quad \text{and} \quad r^{-3}
\]

Discuss this question

Question 7:
The electric potential at a point due to an electric dipole is :

\[k(\overrightarrow{p}.\overrightarrow{r}/r^{3})\]

\[k(\overrightarrow{p}.\overrightarrow{r}/r^{2})\]

\[ k(\overrightarrow{p}\times \overrightarrow{r}/r^{3})\]

\[k(\overrightarrow{p}\times \overrightarrow{r}/r^{2})\]

View Solution

Solution:

The electric potential \( V \) at a point \( P \) due to an electric dipole with dipole moment \( \overrightarrow{p} \) is given by:

\[
V = \frac{k \, \overrightarrow{p} \cdot \overrightarrow{r}}{r^3}
\]

Explanation:
1. Dipole Moment: The dipole moment \( \overrightarrow{p} = q \cdot d \), where \( q \) is the charge and \( d \) is the separation between charges.

2. Position Vector \( \overrightarrow{r} \): This is the vector from the center of the dipole to the point \( P \).

3. Dot Product: The potential depends on the angle between \( \overrightarrow{p} \) and \( \overrightarrow{r} \), hence \( \overrightarrow{p} \cdot \overrightarrow{r} = p r \cos \theta \).

4. Result: The formula is:
\[
V = \frac{k (\overrightarrow{p} \cdot \overrightarrow{r})}{r^3}
\]

This matches the correct answer:
\[
V = \frac{k (\overrightarrow{p} \cdot \overrightarrow{r})}{r^3}
\]

Discuss this question