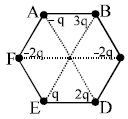
Six charges are placed at the corner of a regular hexagon as shown. If an electron is placed at its centre O , force on it w ill be :
No solution provided for this question.
Six charges are placed at the corner of a regular hexagon as shown. If an electron is placed at its centre O , force on it w ill be :

No solution provided for this question.
When two charges Q each are placed at a distance ‘d’ apart. Find the magnitude of third charge which is placed at mid point the line joining the charge. So that system is in equilibrium
To find the magnitude of the third charge that will keep the system in equilibrium, follow these steps:
Setup:
- Two charges \( Q \) are placed at a distance \( d \) apart.
- A third charge \( q \) is placed at the midpoint of the line joining the two charges.
For the system to be in equilibrium, the net force on all the charges must be zero.
Forces on the third charge \( q \) at the midpoint:
- The two charges \( Q \) exert forces on \( q \) from opposite directions.
- These forces will be equal in magnitude but opposite in direction, so we need to balance them by choosing the right value for \( q \).
Using Coulomb's law, the force between \( Q \) and \( q \) (at a distance \( d/2 \)) is given by:
\[
F = k \frac{|Q \cdot q|}{(d/2)^2} = k \frac{4|Q \cdot q|}{d^2}
\]
Forces on one of the charges \( Q \) (let's take the left charge):
- The charge \( q \) at the midpoint exerts a force on \( Q \) in one direction.
- The other charge \( Q \) exerts a repulsive force on this charge from the opposite direction.
For equilibrium, the force between the two \( Q \)'s must balance the force due to \( q \) on \( Q \).
1. Force between the two \( Q \)'s:
\[
F_{QQ} = k \frac{Q^2}{d^2}
\]
2. Force between \( Q \) and \( q \) (distance \( d/2 \)):
\[
F_{Qq} = k \frac{4|Q \cdot q|}{d^2}
\]
Condition for equilibrium:
The force between the two \( Q \)'s must equal the force between \( Q \) and \( q \):
\[
k \frac{Q^2}{d^2} = k \frac{4|Q \cdot q|}{d^2}
\]
Canceling out the common terms:
\[
Q^2 = 4|Q \cdot q|
\]
\[
q = \frac{Q}{4}
\]
Conclusion:
The magnitude of the third charge \( q \) that should be placed at the midpoint for equilibrium is:
\[
q = \frac{- Q}{4}
\]
Three charges –q1, +q2 and –q3 are placed as shown in figure . The
x-component of the force on –q1 is proportional to
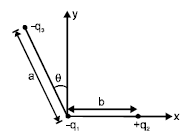
To find the \( x \)-component of the force on charge \(-q_1\) in the given setup, let's break down the forces due to \( +q_2 \) and \( -q_3 \) on \( -q_1 \).
1. Force due to \( +q_2 \):
The force \( F_{12} \) between \( -q_1 \) and \( +q_2 \) acts along the \( x \)-axis (horizontally) and has a magnitude:
\[
F_{12} = \frac{k |q_1| |q_2|}{b^2}
\]
Since this force acts along the positive \( x \)-direction, the \( x \)-component of this force is simply:
\[
F_{12x} = \frac{k |q_1| q_2}{b^2}
\]
2. Force due to \( -q_3 \):
The force \( F_{13} \) between \( -q_1 \) and \( -q_3 \) acts along the line joining them, which makes an angle \( \theta \) with the \( y \)-axis. The magnitude of this force is:
\[
F_{13} = \frac{k |q_1| |q_3|}{a^2}
\]
To find the \( x \)-component of \( F_{13} \), we use the angle \( \theta \) with the \( y \)-axis. The \( x \)-component of \( F_{13} \) is:
\[
F_{13x} = \frac{k |q_1| |q_3|}{a^2} \sin \theta
\]
(positive, as it points in the \( +x \)-direction due to the symmetry).
3. Total \( x \)-component of the force on \( -q_1 \):
Adding the \( x \)-components of both forces, we get:
\[
F_x = F_{12x} + F_{13x} = \frac{k |q_1| q_2}{b^2} + \frac{k |q_1| |q_3|}{a^2} \sin \theta
\]
Final Answer
After dividing by \( k |q_1| \) to find the proportional relation, the \( x \)-component of the force on \( -q_1 \) is proportional to:
\[
\frac{q_2}{b^2} + \frac{q_3}{a^2} \sin \theta
\]
Two spherical conductors B and C having equal radii and carrying equal charges on them repel each other with a force F when kept apart at some distance . A third spherical conductor having same radius as that of B but uncharged is brought in contact with B, the n brought in contact with C and finally removed away from both . The new force of repulsion between B and C is
Given Data
- Two spherical conductors \( B \) and \( C \) have equal radii and equal charges.
- They repel each other with a force \( F \) when kept at a certain distance apart.
Step-by-Step Solution
1. Initial Charge on B and C:
Let's assume the initial charge on both \( B \) and \( C \) is \( q \).
Since they are at a certain distance \( r \) apart, the initial force of repulsion between \( B \) and \( C \) is given by Coulomb's law:
\[
F = \frac{k q^2}{r^2}
\]
2. Introducing the Third Conductor (A):
- A third conductor \( A \) with the same radius as \( B \) and \( C \) is initially uncharged.
- \( A \) is first brought in contact with \( B \), allowing charges to redistribute.
3. Charge Redistribution (First Contact with B):
- When \( A \) (initially uncharged) is brought into contact with \( B \) (which has charge \( q \)), the charge will distribute equally between \( A \) and \( B \) because they have the same radius.
- After contact, the charge on each (both \( A \) and \( B \)) will be:
\[
\frac{q}{2}
\]
4. Charge Redistribution (Then Contact with C):
- Next, \( A \) (which now has charge \( \frac{q}{2} \)) is brought in contact with \( C \) (which has charge \( q \)).
- The charge will again distribute equally between \( A \) and \( C \) because they have the same radius.
- After contact, the charge on each (both \( A \) and \( C \)) will be:
\[
\frac{q}{2} + \frac{q}{2} = \frac{3q}{4}
\]
- So, now \( C \) has a charge of \( \frac{3q}{4} \), and \( A \) also has \( \frac{3q}{4} \).
5. Final Charges on B and C:
- After removing \( A \), the charges on \( B \) and \( C \) are as follows:
- \( B \) has \( \frac{q}{2} \).
- \( C \) has \( \frac{3q}{4} \).
6. New Force of Repulsion between \( B \) and \( C \):
- The new force \( F' \) between \( B \) and \( C \), separated by the same distance \( r \), is given by:
\[
F' = \frac{k \left(\frac{q}{2}\right) \left(\frac{3q}{4}\right)}{r^2}
\]
- Simplifying, we get:
\[
F' = \frac{k \cdot q^2 \cdot 3}{8r^2} = \frac{3}{8} \cdot \frac{k q^2}{r^2}
\]
- Since \( F = \frac{k q^2}{r^2} \), we can write:
\[
F' = \frac{3}{8} F
\]
Final Answer
The new force of repulsion between \( B \) and \( C \) is:
\[
\frac{3F}{8}
\]
When 2 point charges +q and +3q are held at a distance r from each other are released, they have an acceleration of a and 2a respectively. When we distribute the total charge equally between them , keep them at same distance as the original and release them , their accelerations now would be:
Initial Setup:
1. Charges and Forces:
- Two charges \( +q \) and \( +3q \) are separated by distance \( r \).
- The force between them initially is:
\[
F = \frac{k \cdot q \cdot 3q}{r^2} = \frac{3kq^2}{r^2}
\]
2. Accelerations:
- Let the masses of the charges be \( m_1 \) and \( m_2 \).
- Given that the initial accelerations are \( a \) and \( 2a \) for charges \( +q \) and \( +3q \) respectively, we have:
\[
F = m_1 a \quad \text{and} \quad F = m_2 \cdot 2a
\]
Step 1: Determine Mass Ratio
From the equations \( m_1 a = m_2 \cdot 2a \), we get:
\[
m_2 = \frac{m_1}{2}
\]
Step 2: New Charges After Redistribution
When the total charge \( q + 3q = 4q \) is equally distributed, each charge will be:
\[
\frac{4q}{2} = 2q
\]
Step 3: New Force Between Charges
With the new charges \( +2q \) and \( +2q \) at the same distance \( r \), the new force \( F' \) is:
\[
F' = \frac{k \cdot 2q \cdot 2q}{r^2} = \frac{4kq^2}{r^2}
\]
Step 4: New Accelerations
Using \( F' = m_1 a_1' \) and \( F' = m_2 a_2' \), we get:
1. For the first charge (\( m_1 \)):
\[
a_1' = \frac{F'}{m_1} = \frac{4kq^2 / r^2}{m_1} = \frac{4a}{3}
\]
2. For the second charge (\( m_2 = \frac{m_1}{2} \)):
\[
a_2' = \frac{F'}{m_2} = \frac{4kq^2 / r^2}{m_1 / 2} = \frac{8a}{3}
\]
Answer
The new accelerations are:
\[
\frac{4a}{3} \quad \text{and} \quad \frac{8a}{3}
\]
Two conducting sphere s of radii R each are given charges +Q and –Q and are separated by a distance r (>2R). Th e force of attraction between them is \( \overrightarrow{F} \)If instead of charges +Q and –Q, we were to give them charges +Q each , the force of interaction between them would be
When the spheres have charges \( +Q \) and \( -Q \), they attract each other with force \( \overrightarrow{F} \).
If we replace \( -Q \) with \( +Q \), both spheres will have \( +Q \) charge, causing a repulsive force instead of attraction.
Since \( r > 2R \), there will be induced charges on the surfaces due to electrostatic induction, reducing the effective repulsive force compared to the attractive force \( \overrightarrow{F} \) in the initial configuration.
Conclusion:
The new force will be in the opposite direction to \( \overrightarrow{F} \) (repulsive) but with a magnitude less than \( F \) due to the effect of induced charges.
Three charged particles are placed on a straight line as shown in Fig. q1 and q2 are fixed, but q3 can be moved. Under the action of the forces from q1 and q2, q3 is in equilibrium. What is the relation between q1 and q2?
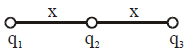
To find the relation between \( q_1 \) and \( q_2 \) for \( q_3 \) to be in equilibrium, let's analyze the forces on \( q_3 \).
1. Forces on \( q_3 \):
- The force due to \( q_1 \) on \( q_3 \) is:
\[
F_{13} = \frac{k |q_1| |q_3|}{(2x)^2} = \frac{k |q_1| |q_3|}{4x^2}
\]
(directed towards \( q_1 \) if \( q_1 \) and \( q_3 \) have opposite signs).
- The force due to \( q_2 \) on \( q_3 \) is:
\[
F_{23} = \frac{k |q_2| |q_3|}{x^2}
\]
(directed towards \( q_2 \) if \( q_2 \) and \( q_3 \) have opposite signs).
2. Equilibrium Condition for \( q_3 \):
For \( q_3 \) to be in equilibrium, these forces must be equal in magnitude:
\[
F_{13} = F_{23}
\]
Substituting the values:
\[
\frac{k |q_1| |q_3|}{4x^2} = \frac{k |q_2| |q_3|}{x^2}
\]
Cancelling \( k \), \( |q_3| \), and \( x^2 \) from both sides, we get:
\[
\frac{|q_1|}{4} = |q_2|
\]
Therefore:
\[
q_1 = -4q_2
\]
Answer:
The relation between \( q_1 \) and \( q_2 \) is:
\[
q_1 = -4q_2
\]
Two particles A and B (B is right of A) having charges \( 8\times 10^{-6}C \)and ( -2\times 10^{-6}C\), respectively, are held fixed with separation of 20 cm. Where should a third charged particle be placed so that it does not experience a net electric force :
Let's solve this briefly.
1. Charges and Positions:
- Charge on \( A = 8 \times 10^{-6} \, \text{C} \).
- Charge on \( B = -2 \times 10^{-6} \, \text{C} \).
- Distance between \( A \) and \( B = 20 \, \text{cm} \).
2. Equilibrium Condition for Third Charge \( Q \):
- For the third charge \( Q \) to experience zero net force, it must be positioned where the attractive force from \( A \) and the repulsive force from \( B \) on \( Q \) are equal in magnitude.
- Since \( |A| > |B| \), \( Q \) must be placed on the right side of \( B \) (further from \( A \)).
3. Distance Calculation:
- Let the distance of \( Q \) from \( B \) be \( x \).
- The distance of \( Q \) from \( A \) is then \( 20 + x \).
Using Coulomb's law, we set the magnitudes of the forces equal:
\[
\frac{k \cdot (8 \times 10^{-6}) \cdot Q}{(20 + x)^2} = \frac{k \cdot (2 \times 10^{-6}) \cdot Q}{x^2}
\]
Simplify by cancelling \( k \) and \( Q \):
\[
\frac{8}{(20 + x)^2} = \frac{2}{x^2}
\]
Cross-multiplying gives:
\[
8x^2 = 2(20 + x)^2
\]
Simplifying, we find \( x = 20 \, \text{cm} \).
Answer:
The third charge should be placed 20 cm to the right of \( B \) for zero net force.
Two point charges repel each other with a force of 100 N. One of the charges is increased by 10%, and the other is reduced by 10%. The new force of repulsion at the same distance would be :-
The initial force \( F \) between two charges \( q_1 \) and \( q_2 \) is given by:
\[
F = k \frac{q_1 q_2}{r^2} = 100 \, \text{N}
\]
After changing the charges:
- \( q_1 \) increases by 10%, so \( q_1' = 1.1 q_1 \).
- \( q_2 \) decreases by 10%, so \( q_2' = 0.9 q_2 \).
The new force \( F' \) is:
\[
F' = k \frac{q_1' q_2'}{r^2} = k \frac{(1.1 q_1)(0.9 q_2)}{r^2} = (1.1 \times 0.9) F
\]
Calculating \( 1.1 \times 0.9 = 0.99 \), so:
\[
F' = 0.99 \times 100 = 99 \, \text{N}
\]
An isolated charge q1 of mass m is suspended freely by a thread of length l. Another charge q2 is brought near it (r >>l). When q1 is equilibrium, tension in thread will be :
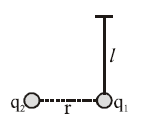
Solution Outline:
1. Forces Acting on \( q_1 \):
- Gravitational Force: \( F_g = mg \), acting vertically downward.
- Electrostatic Force: \( F_e = \frac{k |q_1 q_2|}{r^2} \), acting horizontally toward \( q_2 \).
2. Resultant Tension \( T \)
Since \( q_1 \) is in equilibrium, the tension \( T \) in the thread must balance both the gravitational and electrostatic forces. The tension will act diagonally, with components to counteract both the vertical \( mg \) and horizontal \( F_e \) forces.
3. Calculating \( T \):
Using vector addition, we find \( T \) as:
\[
T = \sqrt{(mg)^2 + \left( \frac{k |q_1 q_2|}{r^2} \right)^2}
\]
Since \( \frac{k |q_1 q_2|}{r^2} \) is a positive quantity, \( T \) is indeed greater than \( mg \).
Conclusion:
The correct answer is:
\[
T > mg
\]