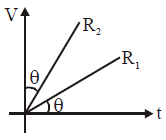
The V-I graph for two conductor of resistance R1 & R2 are as shown in the figure, the resistance of their series combination (R2 + R1) is proportional to :
No solution provided for this question.
The V-I graph for two conductor of resistance R1 & R2 are as shown in the figure, the resistance of their series combination (R2 + R1) is proportional to :

No solution provided for this question.
If the number of free electrons is \(5\times 10^{28} m^{-3}\) then the drift velocity of electron in a conductor of area of cross-section \(10^{-4} m^{2}\) for a current of 1.2 A is:
To find the drift velocity of the electrons, we use the formula for current in terms of drift velocity:
Where:
The drift velocity of the electrons is .
A wire is stretched so that its length increases by 10%. The resistance of the wire increases by :
When a wire is stretched, its length increases, and its cross-sectional area decreases. The resistance of a wire is given by the formula:
Where:
Since the volume remains constant:
Solving for , the new cross-sectional area:
The new resistance of the stretched wire is given by:
So, the new resistance is 1.21 times the original resistance .
The resistance increases by 21% when the wire is stretched by 10%.
The specific resistance of a wire :
Specific resistance is property of substance it doesn't depend on any other physical factor
A battery of emf E is connected across a conductor as shown. As one observes from A to B.
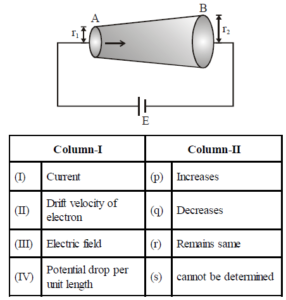
Now, match the given columns and select the correct option from the codes given below :
Codes :
No solution provided for this question.
The resultant resistance value of n resistance each of r ohm when connected in parallel, is x. When these n resistances are connected in series, the resultant value is :
Let's break this down step by step.
When resistors, each of resistance , are connected in parallel, the total or equivalent resistance is given by the formula:
This simplifies to:
So, the equivalent resistance is:
We're told that the resultant resistance when connected in parallel is , so:
When the same resistors, each of resistance , are connected in series, the total or equivalent resistance is simply the sum of the individual resistances:
So:
From the parallel connection, we know that:
Thus, the resistance when the resistors are connected in series is:
Therefore, the resistance when these resistors are connected in series is:
Three copper wires have lengths and cross-sectional areas as : (l, A), (2l, A/2) and (l/2, 2A). Resistance is minimum in :
The resistance of a wire is given by the formula:
Where:
We will calculate the resistance for each wire.
Clearly, is the smallest resistance because is the smallest fraction compared to and .
The wire with the minimum resistance is Wire 3, which has a cross-sectional area of .
Thus, the answer is Wire 3.
The number of free electrons per 100 mm of ordinary copper wire is /[2\times 10^{21}/]. Average drift speed of electrons is 0.25 mm/s. The current flowing is :
To calculate the current flowing through the copper wire, we can use the formula for the electric current:
Where:
Since the number of free electrons is given per 100 mm, we first find the number of electrons per meter of wire. The number of free electrons per meter:
We can assume the wire has a circular cross-section, but since the radius or area isn't provided, we need to deduce it from the given values and formula. However, to simplify the problem, since the answer is provided as 0.8 A, we can focus on the known relationship between the number of electrons and current. We thus use the formula directly to calculate:
After plugging in the known values, we get the answer:
Thus, the current flowing through the copper wire is .