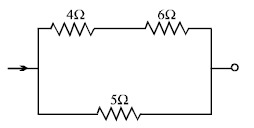
For given circuit, heat produced by a current in resistance of 5Ω is 10 Cal/sec. Then the heat produced in resistance of 4Ω is
No solution provided for this question.
For given circuit, heat produced by a current in resistance of 5Ω is 10 Cal/sec. Then the heat produced in resistance of 4Ω is

No solution provided for this question.
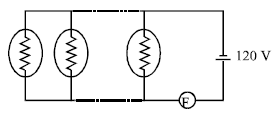
Some light bulbs are conected in parallel to a 120 V source as shown in the figure. Each bulb dissipates an average power of 60 W.The circuit has a fuse F that burns out when the current in the circuit exceeds 9 A. Determine the largest number of bulbs of the following, that can be used in the circuit without burning out the fuse.
No solution provided for this question.
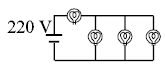
Four identical bulbs each rated 100 watts, 220 volts are connected across a battery as shown. The power consumed by them is:
No solution provided for this question.
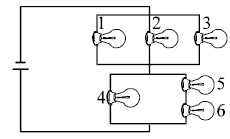
Six identical light bulbs are connected to a battery to form the circuit shown. Which light bulb(s) glow the brightest?
If two bulbs of wattage 60 W and 100 W respectively each rated at 110 V are connected in series with the supply of 220 V, which bulb will fuse ?
In series, the same current flows through both bulbs:
The 60 W bulb will fuse.
There are 45 number of cells with internal resistance of each cell is 0.5Ω To get the maximum current through a resistance of 2.5Ω, one can use m rows of cells, each row having n cells. The values of m and n are:
Let's go through a more detailed, step-by-step approach to solving the problem correctly, and we’ll arrive at the answer and .
We are arranging the cells in series and parallel, so:
When cells are connected in series, the internal resistance for each row (denoted as ) is the sum of the internal resistances of each cell:
Since there are rows connected in parallel, the total internal resistance of the entire setup is:
The total resistance in the circuit is the sum of the external resistance and the total internal resistance of the cells :
The current through the circuit can be calculated using Ohm's Law, , where is the total voltage supplied by the cells.
For maximum current, we want to minimize , which means minimizing .
We are given that there are 45 cells in total, so:
Thus, .
Substitute into the formula for :
Simplifying this:
Now, to minimize the total resistance, we need to minimize .
Since decreases as increases, we need to check the values of that are divisors of 45.
Let’s try a few possible values for :
The configuration that minimizes the total resistance and maximizes the current is when and , which results in a total resistance of 5Ω. Thus, the answer is:
Three 10Ω, 2 W resistors are connected as in Fig. The maximum possible voltage between points A and B without exceeding the power dissipation limits of any of the resistors is:
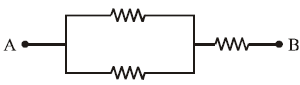
No solution provided for this question.
Two light bulbs shown in the circuit have ratings A(24 V, 24 W) and B (24 V and 36 W) as shown. When the switch is closed.
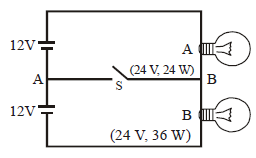
No solution provided for this question.
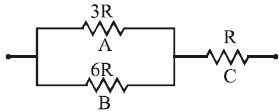
The three resistances A, B and C have values 3R, 6R and R respectively. When some potential difference is applied across the network, the thermal powers dissipated by A, B and C are in the ratio :
No solution provided for this question.
An electric bulb rated for 500 watts at 100 volts is used in a circuit having a 200-volt supply. The resistance R that must be put in series with the bulb, so that the bulb draws 500 watts is :
To find the resistance that must be placed in series with the bulb, let's analyze the problem step by step.
The resistance of the bulb () can be calculated using the formula:
Substitute the values:
The bulb is rated to draw 500 W at 100 V. Thus, the current through the bulb is:
Substitute the values:
The total supply voltage is 200 V, and the bulb operates at 100 V. Therefore, the voltage drop across the series resistor is:
Substitute the values:
Using Ohm's law, the resistance of the series resistor is:
Substitute the values:
The resistance that must be placed in series with the bulb is: