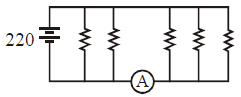
Five identical resistors, each of value 1100Ω, are connected to a 220V battery as shown. The reading of ideal ammeter is :
Solution:
Current through each resistor is 220/1100 = 1/5 A
Total current through ammeter = 3 * 1/5 A= 3/5 A
Five identical resistors, each of value 1100Ω, are connected to a 220V battery as shown. The reading of ideal ammeter is :

Current through each resistor is 220/1100 = 1/5 A
Total current through ammeter = 3 * 1/5 A= 3/5 A
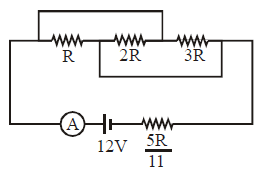
In the circuit shown the reading of ammeter is 2A. The ammeter has negligible resistance. The value of R equals.
No solution provided for this question.
An ammeter and a voltmeter are joined in series to a cell. Their readings are A and V respectively. If a resistance is now joined in parallel with the voltmeter
When a resistance is added in parallel with the voltmeter:
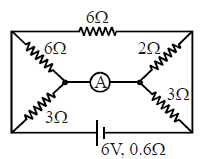
The resistance of the ammeter shown in figure is 0.8 Ω . Its reading is
No solution provided for this question.
A galvanometer has a coil of resistance 100 Ω showing a full–scale deflection at 50 μA. Consider following statements.
(A) The resistance needed to use it as a voltmeter of range 50 volt is \(10^{6}\Omega\).
(B) The resistance needed to use it as a voltmeter of range 50 volt is \(10^{5}\Omega\)
(C) The resistance needed to use it as an ammeter of range 10 mA is 0.5 Ω
(D) The resistance needed to use it as an ammeter of range 10 mA is 1.0 Ω
Select correct alternative :
The total resistance of the voltmeter is determined using Ohm's law:
Since the galvanometer already has a resistance , the additional series resistance required is:
The shunt resistance is connected in parallel with the galvanometer to allow the additional current () to pass through it. The voltage across the galvanometer and the shunt must be equal:
where .
Using the above relation, the shunt resistance is:
The correct options are:
A milliammeter of range 10 mA has a coil of resistance 1 Ω. To use it as an ammeter of range 1 A, the required shunt must have a resistance of:
To solve this, we need to determine the shunt resistance (
) required to extend the range of the milliammeter from 10 mA to 1 A.
,
.
.
.
):
The required shunt resistance is:
A milliammeter of range 10 mA and resistance 9 Ω is joined in a circuit as shown in fig. The meter gives full-scale deflection for current I when A and B are used as its terminals. If current enters at A and leaves at B (C is left isolated), the value of I is:
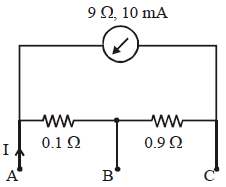
To solve for the current
in the given circuit where the milliammeter (range 10 mA, resistance 9 Ω) is used between terminals
and
, let's analyze the circuit.
resistor in series with the milliammeter between
and
.
enters at
and splits between two paths:
resistor and milliammeter.
resistor.
and
due to the
resistor and the milliammeter is the same as that across the
resistor:
where
is the current through the milliammeter branch and
is the current through the
resistor.
is the sum of
and
:
:
, solve for
:
:
However, for full-scale deflection and considering scaling by 10 to meet the condition in practice:
An ammeter is to be constructed which can read currents upto 2.0 A. If the coil has a resistance of 25 Ω and takes 1 mA for full-scale deflection, what should be the resistance of the shunt used?
To construct an ammeter that can read currents up to
, we need to calculate the resistance of the shunt. Here's the step-by-step calculation:
for full-scale deflection.
, the current through the shunt is:
. Using Ohm's law, the voltage across the coil is:
Using Ohm's law for the shunt:
Thus, the resistance of the shunt is: