A wheel having diameter of 3 m starts from rest and accelerates uniformly to an angular velocity of 210 rpm in 5 seconds. Angular acceleration of the wheel is :
Question 1:
Uniform Circular Motion
Question 2:
The angular velocity of earth about its axis of rotation is :
Question 3:
Two bodies of masses 10 kg and 5 kg moving on concentric orbits of radii R and r such that their period of revolution are same. The ratio of their centripetal acceleration is :
Solution:
As time period of revolution is same for both the particles angular speed will be equal for both.
Centripetal Acceleration is given by ω²r.
so a 1 / a 2 = R/r
Question 4:
A stone of mass m is tied to a string of length l and rotated in a circle with a constant speed v. If the string is released, the stone flies :
Solution:
In Circular motion velocity of the particle is always directed along tangent. So when string is released object moves tangentially.
Question 5:
A stone of mass 1 kg tied to one end of a string 1.0 m long is revolved in a horizontal circle at the rate of 10/π revolution per second. Calculate the tension of the string ?
Solution:
Tension force in the string will provide required centripetal force
T = mω²r= 1× (10/π ×2π)²×1= 400 N
Question 6:
Find ratio of Normal reaction of blocks. At point A & point B respectively if their masses are same and velocities are 2 m/s & 4 m/s respectively :
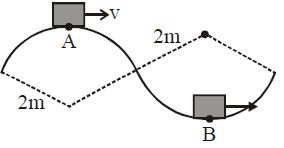
Solution:
Centrifugal Force act radially outwards,
So, N A = mg - mv²/R = m(10) - m(2)²/2= 8m
So, N B = mg + mv²/R = m(10) +m(4)²/2= 18m
N A : N B = 4 : 9
Question 7:
Two stones of masses m and 2 m are whirled in horizontal circles, the heavier one in a radius r/2 and the lighter one in radius r. The tangential speed of lighter stone is n times that of the value of heavier stone when they experience same centripetal forces. The value of n is :
Question 8:
A particle moves in a circle of radius 5 m with constant speed and time period 2π s. The acceleration of the particle is :
Solution:
As speed of the particle is constant only centripetal acceleration will act on the object.
Centripetal Acceleration = ω²R
a c = (2π/2π)× 5= 5 m/s²