Kinematics of Circular Motion – Rankers Physics
← Back to Circular Motion

Kinematics of Circular Motion

Question 1:

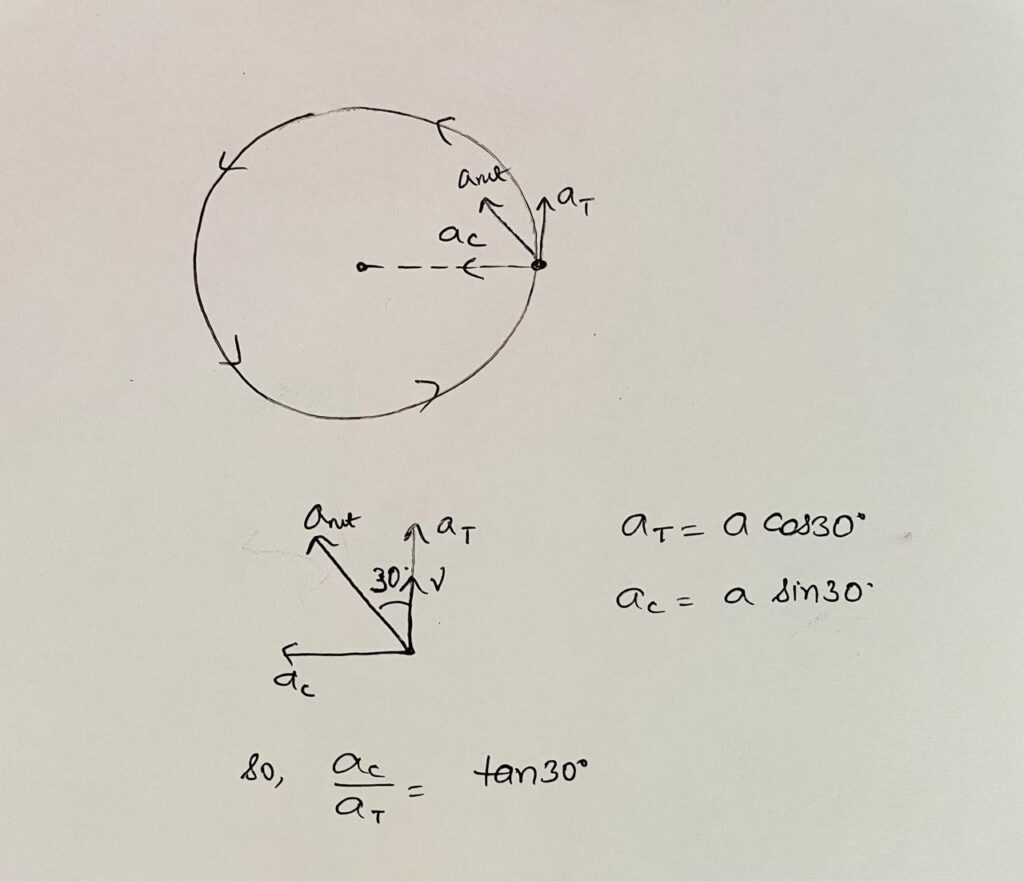
A point on the periphery of rotating disc has its acceleration vector making on angle 30° with velocity vector then the ratio of magnitude of centripetal acceleration to tangential acceleration is :

sin 30°
cos 30°
tan 30°
None of these
View Solution

Solution:

Discuss this question

Question 2:

A stone is moved round a horizontal circle with a 20 cm long string tied to If centripetal acceleration is 9.8 m/s2, then its angular velocity will be :

7 rad/s
22/7 rad/s
49 rad/s
14 rad/s
View Solution

Solution:

Centripetal Acceleration is given by a= ω²R

⇒ 9.8 = ω²× 1/5

⇒ ω² =49

⇒ ω = 7 rad/sec

Discuss this question

Question 3:

A block on a stationary horizontal table with increasing speed in a circle is seen from an inertial frame of reference. The   angle between net force on the block and velocity vector is :

Greater than 90°
Less than 90°
Equal to 90°
Data is insufficient
View Solution

Solution:

When net acceleration makes acute angle with velocity, speed of the particle will increase. As tangential accleration is positive, speed will increase.

Discuss this question

Question 4:

A wheel is subjected to uniform angular acceleration about its axis. Initially its angular velocity is zero.  In the first 2 sec, it rotates through an angle θ1; in the next 4 sec, it rotates through an additional angle θ2. The ratio of θ2/θ1 is :

9
2
3
8
View Solution

Solution:

For Circular motion angle traversed is θ = ω t + ½ α t²

so, θ1   =½α(2)² = 2α

and θ1 + θ2 = ½α(6)² = 18 α ⇒ θ2= 16 α

so θ2 /θ1= 8

Discuss this question

Question 5:

A wheel having diameter of 3 m starts from rest and accelerates uniformly to an angular velocity of 210 rpm in 5 seconds. Angular acceleration of the wheel is :

1.4π rad/s²
3.3π rad/s²
2.2π rad/s²
1.1π rad/s²
View Solution

Solution:

ω = ω + α . t 

⇒(210 × 2π)/60 = 0 + α × 5 

⇒ α = 1.4 π rad/sec ²

Discuss this question

Question 6:

The angular velocity of earth about its axis of rotation is :

2π/(60×60×24) rad/sec
2π/(60×60) rad/sec
2π/60 rad/sec
2π/(365×24×60×60) rad/sec
View Solution

Solution:

Angular speed ω = 2π / T = 2π / (60×60×24) rad /sec 

Discuss this question

Question 7:

A spot light S rotates in a horizontal plane with a constant angular velocity of 0.1 rad/s. The spot of light P moves along the wall at a distance of 3 m. The velocity of spot P when θ = 45° is :-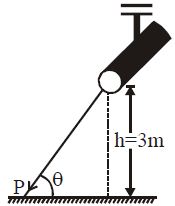

0.2 m/s
0.3 m/s
0.6 m/s
0.8 m/s
View Solution

No solution provided for this question.

Question 8:

At t = 0 a wheel is rotating at 50 rad/sec. A motor gives it a constant angular acceleration of 5 rad/sec2 until it reaches 100 rad/sec the motor is disconnected how many revolutions are completed at t = 20 sec 

1250
625
625/π
875/π
View Solution

Solution:

ω = ω 0 + α.t

⇒ 100 =50 + 5 × t

⇒ 50 = 5.t

⇒ t = 10 sec.

Angle traversed during acceleration= ½.α.t²= ½×5×(10)²= 250 rad

Angle traversed with constant angular speed = ω.t= 100 × 10 = 1000 rad

Total angle traversed = 1250 rad 

Number of Revolutions = 1250 /2π= 625 /π 

Discuss this question