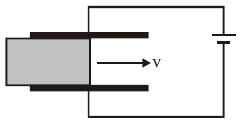
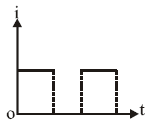
 The capacitor is connected to a battery of emf E. The current in the circuit varies with time as
The capacitor is connected to a battery of emf E. The current in the circuit varies with time asSolution:
To plot a graph for the current versus time , let's break the problem into steps:
1. Capacitor with Dielectric Slab
- Initial Configuration: The capacitor has plates of total area and plate separation . It is connected to a battery with emf .
- Dielectric Slab: A dielectric slab of area is inserted at a constant speed .
2. Capacitance with Partial Dielectric
When a dielectric is partially inserted into the capacitor, the total capacitance is the sum of two capacitors:
- One part with the dielectric slab ().
- One part without the dielectric slab ().
Capacitance of the two regions:
- With Dielectric Slab:
where is the dielectric constant.
- Without Dielectric Slab:
Thus, the total capacitance is:
3. Change in Capacitance with Time
As the slab moves with speed , the area covered by the slab changes with time:
The effective capacitance changes as:
Simplify:
4. Current in the Circuit
The current in the circuit is related to the rate of change of capacitance:
Differentiate with respect to :
Thus:
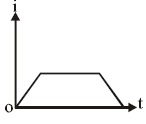
5. Graph of vs.
The current is constant because it does not depend on (the rate of capacitance change is constant). Hence, the graph of vs. will be a horizontal line at:
Leave a Reply