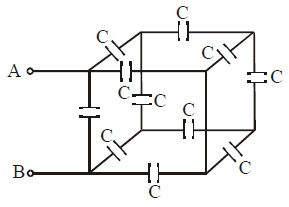
Solution:

To find the equivalent capacitance for this cubical capacitor network, where each edge of the cube has a capacitance $C$, here’s the shortest solution:

Step-by-Step:

1. Symmetry analysis:
   • By symmetry, all corners of the cube can be grouped into equivalent potential nodes.
   • The cube's symmetry allows reduction to a simpler circuit.
2. Key nodes:
   • Node $A$ is connected to one corner of the cube.
   • Node $B$ is connected to the diagonally opposite corner.
3. Effective connections:
   • Due to symmetry, three capacitors are effectively in parallel between $A$ and an intermediate point.
   • Similarly, three capacitors are effectively in parallel between $B$ and the same intermediate point.
   • Two capacitors remain directly between $A$ and $B$.
4. Simplification:
   • The three parallel capacitors at each node result in: $$C_{\text{parallel}} = 3C$$
   • The equivalent circuit becomes two $3C$ capacitors in series with a $2C$ capacitor: $$\text{Series combination:} \quad \frac{1}{C_{\text{eq}}} = \frac{1}{3C} + \frac{1}{3C} + \frac{1}{2C}$$
5. Calculation:
   • Combine series: $$\frac{1}{C_{\text{eq}}} = \frac{2}{3C} + \frac{1}{2C} = \frac{4}{6C} + \frac{3}{6C} = \frac{7}{6C}$$
   • Invert to find $C_{\text{eq}}$: $$C_{\text{eq}} = \frac{6C}{7} \times 2 = \frac{12C}{7}$$

Thus, the equivalent capacitance is:

$$C_{\text{eq}} = \frac{12C}{7}$$