The density of the atmosphere at sea level is 1.3 kg/m3. Assume it does not change with altitude and g = 10 ms–2, how high would the atmosphere extend ?
No solution provided for this question.
The density of the atmosphere at sea level is 1.3 kg/m3. Assume it does not change with altitude and g = 10 ms–2, how high would the atmosphere extend ?
No solution provided for this question.
A tube 1 cm2 in cross-section is attached to the top of a vessel 1 cm high and of cross-section 100 cm2. Water is poured into the system filling it to a depth of 100 cm above the bottom of the vessel as shown in figure. Take g = 10 ms–2. Now,
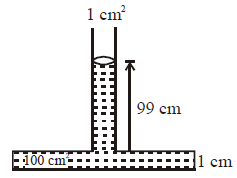
No solution provided for this question.
A ball floats on the surface of water in a container exposed to the atmosphere. When the container is covered and the air is partially removed, then the ball : [Consider buoyancy effect of air also]
No solution provided for this question.
A body with a volume V neither sinks nor floats in a liquid. If the vessel containing the liquid falls with an acceleration g/3 , then the volume of the
solid inside the liquid in the falling condition is:-
No solution provided for this question.
A cylindrical piece of cork of density \[\rho\] of base area A and height h floats in a liquid of density \[\rho\acute{}\]. The cork is slightly depressed and then released. The time period of oscillation of the cork is :-
No solution provided for this question.
A cubical box of wood of side 30 cm weighing 21.6 kg floats on water with two faces horizontal. Calculate the depth of immersion of wood.
No solution provided for this question.
A sample of metal weights 210 gram in air, 180 gram in water and 120 gram in an unknown liquid. Then:-
No solution provided for this question.
Two non-mixing liquids of densities \[\rho\] and \[n\rho(n>1)\] are put in a container. The height of each liquid is h. A solid cylinder of length L and density d is put in this container. The cylinder floats with its axis vertical and length pL(p < 1) in the denser liquid. The density d is equal to :-
No solution provided for this question.
A tank contains water on top of mercury as shown in figure. A cubical block of side 10 cm is in equilibrium inside the tank. The depth of the block inside mercury is (RD of the material of block = 8.56, RD of mercury = 13.6)
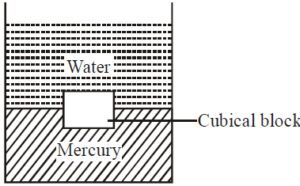
No solution provided for this question.
The reading of spring balance when a block is suspended from it in air, is 60 N. This reading is changed to 40 N when the block is immersed in water. The specific gravity of the block is :
No solution provided for this question.