The mass M shown in the figure oscillates in simple harmonic motion with amplitude A. The amplitude of the point P is :
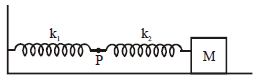
No solution provided for this question.
Question 1:
Spring Block System
Question 2:
One end of an ideal spring is fixed with a wall and the other end is fixed with a block of mass 1 kg. Force constant of spring is 100 N/m and block is performing S.H.M. with amplitude 3 cm. When the block is at left extreme position, another block of mass 3 kg moving directly towards 1 kg block with velocity 80/3 cm/s collides and gets stuck to it. The amplitude of oscillation of the combined body is :
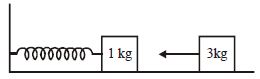
No solution provided for this question.
Question 3:
A block P of mass m is placed on a frictionless horizontal surface. Another block Q of same mass is kept on P and connected to the wall with the help of a spring of spring constant k as shown in the figure. μs is the coefficient of friction between P and Q. The blocks move together performing simple harmonic motion with amplitude A. The
maximum value of the friction force between P and Q is :
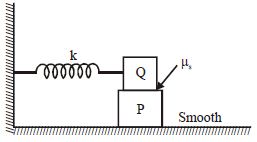
No solution provided for this question.
Question 4:
A mass M is suspended from a spring of negligible mass. The spring is pulled a little and
then released so that the mass executes SHM of time period T. If the mass is increased by m, the time period becomes 5T/3. Then the ratio of m/M is :
Solution:
1. Initial Time Period:
\[
T = 2\pi \sqrt{\frac{M}{k}}
\]
2. New Time Period:
\[
\frac{5T}{3} = 2\pi \sqrt{\frac{M + m}{k}}
\]
3. Divide the New Time Period by the Initial Time Period:
\[
\frac{\frac{5T}{3}}{T} = \sqrt{\frac{M + m}{M}}
\]
\[
\frac{5}{3} = \sqrt{\frac{M + m}{M}}
\]
4. Square Both Sides:
\[
\frac{25}{9} = \frac{M + m}{M}
\]
5. Solve for \( \frac{m}{M} \):
\[
\frac{m}{M} = \frac{25}{9} - 1 = \frac{16}{9}
\]
Answer:
\[
\frac{m}{M} = \frac{16}{9}
\]
Question 5:
In figure S1 and S2 are identical springs. The oscillation frequency of the mass m is f. If one spring is removed, the frequency will become :
Solution:
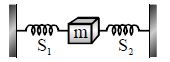
Given that \( S_1 \) and \( S_2 \) are identical springs, they each have the same spring constant \( k \). When both springs are attached, they are in parallel, so the effective spring constant \( k_{\text{eq}} \) is:
\[
k_{\text{eq}} = k + k = 2k
\]
The frequency \( f \) of oscillation for mass \( m \) with effective spring constant \( k_{\text{eq}} = 2k \) is:
\[
f = \frac{1}{2\pi} \sqrt{\frac{2k}{m}}
\]
If One Spring is Removed
If one spring is removed, only one spring with constant \( k \) is left. The new frequency \( f' \) becomes:
\[
f' = \frac{1}{2\pi} \sqrt{\frac{k}{m}}
\]
Ratio of New Frequency to Original Frequency
\[
\frac{f'}{f} = \frac{\frac{1}{2\pi} \sqrt{\frac{k}{m}}}{\frac{1}{2\pi} \sqrt{\frac{2k}{m}}} = \frac{\sqrt{\frac{k}{m}}}{\sqrt{\frac{2k}{m}}} = \frac{1}{\sqrt{2}}
\]
Thus:
\[
f' = \frac{f}{\sqrt{2}}
\]
Answer: \( f' = \frac{f}{\sqrt{2}} \)
Question 6:
Four massless springs whose force constants are 2k, 2k, k and 2k respectively are attached to a mass M kept on a frictionless plane (as shown in figure). If the mass M is displaced in the horizontal direction, then the frequency of oscillation of the system is :
Solution:
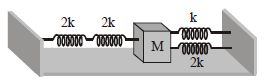
1. Left Side:
- Two springs with spring constants \( 2k \) and \( 2k \) are in series.
- The combined spring constant \( k_{\text{left}} \) for these two springs in series is:
\[
\frac{1}{k_{\text{left}}} = \frac{1}{2k} + \frac{1}{2k} = \frac{1}{k}
\]
\[
k_{\text{left}} = k
\]
2. Right Side:
- Two springs with spring constants \( k \) and \( 2k \) are in parallel.
- The combined spring constant \( k_{\text{right}} \) for these two springs in parallel is:
\[
k_{\text{right}} = k + 2k = 3k
\]
3. Combine Left and Right Sides:
- Since \( k_{\text{left}} \) and \( k_{\text{right}} \) are in parallel, the equivalent spring constant \( k_{\text{eq}} \) is:
\[
k_{\text{eq}} = k_{\text{left}} + k_{\text{right}} = k + 3k = 4k
\]
Step 2: Calculate the Frequency of Oscillation
The frequency \( f \) is given by:
\[
f = \frac{1}{2\pi} \sqrt{\frac{k_{\text{eq}}}{M}}
\]
Substitute \( k_{\text{eq}} = 4k \):
\[
f = \frac{1}{2\pi} \sqrt{\frac{4k}{M}}
\]
Final Answer
\[
f = \frac{1}{2\pi} \sqrt{\frac{4k}{M}}
\]
Question 7:
A force of 6.4 N stretches a vertical spring by 0.1 m. The mass that must be suspended from the spring so that it oscillates with a time period of π/4 second :
Solution:
Given:
- Force \( F = 6.4 \, \text{N} \)
- Extension \( x = 0.1 \, \text{m} \)
- Time period \( T = \frac{\pi}{4} \, \text{s} \)
1. Find the spring constant \( k \):
\[
k = \frac{F}{x} = \frac{6.4}{0.1} = 64 \, \text{N/m}
\]
2. Use the formula for the time period of a mass-spring system:
\[
T = 2\pi \sqrt{\frac{m}{k}}
\]
Substitute \( T = \frac{\pi}{4} \) and \( k = 64 \):
\[
\frac{\pi}{4} = 2\pi \sqrt{\frac{m}{64}}
\]
3. Solve for \( m \):
\[
\frac{1}{8} = \sqrt{\frac{m}{64}}
\]
\[
\frac{1}{64} = \frac{m}{64}
\]
\[
m = 1 \, \text{kg}
\]
Answer: \( m = 1 \, \text{kg} \)
Question 8:
What is the angular frequency of the system shown in the figure?
Solution:
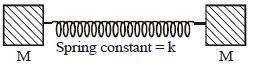
The system shown consists of two masses \( M \) connected by a spring with a spring constant \( k \). Since the masses are identical, the angular frequency \( \omega \) of the system for oscillations is given by:
\[
\omega = \sqrt{\frac{k}{\text{reduced mass}}}
\]
In this case, the reduced mass \( \mu \) of the system is given by:
\[
\mu = \frac{M \cdot M}{M + M} = \frac{M}{2}
\]
Thus, the angular frequency \( \omega \) is:
\[
\omega = \sqrt{\frac{k}{M/2}} = \sqrt{\frac{2k}{M}}
\]
Answer:
\[
\omega = \sqrt{\frac{2k}{M}}
\]