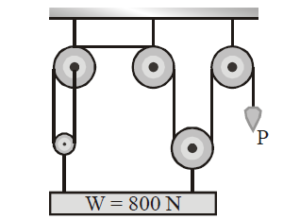
For the arrangement of pulleys shown in figure the effort (P) required to raise the given load (W) is
Solution:
Net Force acting on the block in upward direction is 4T which will balance weight of the object. So,
⇒ 4T= 800 N
⇒T = 200 N
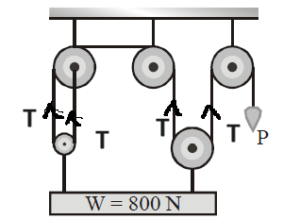
For the arrangement of pulleys shown in figure the effort (P) required to raise the given load (W) is


Net Force acting on the block in upward direction is 4T which will balance weight of the object. So,
⇒ 4T= 800 N
⇒T = 200 N
What are the acceleration of the blocks A and B, shown in figure (in m/sec²)
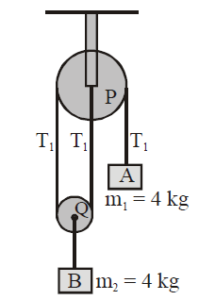
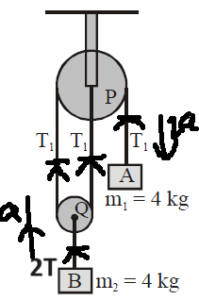
Writing equations of motion for the objects as,
40 - T = 4 × 2a ---(i)
and 2T -40 = 4a -----(ii)
Solving (i) and (ii)
a= 2 m/s²
So, acceleration of object A is 4 m/s² and for object B is 2 m/s²
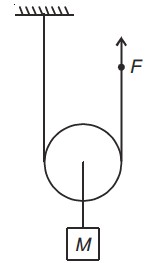
The masses of the bodies A and B in figure are 20 kg and 10 kg, respectively. They are initially at rest on the floor and are connected by a weightless string passing over a weightless and frictionless pulley. An upward force F is applied to the pulley. Find the acceleration a1 of body A and a2 of body B when F is 340 N :
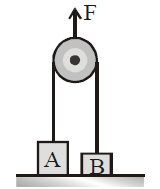
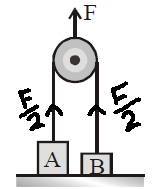
As F= 340 N. Force acting on object A in upward direction is F/2 i.e 170 N. This force is insufficient to pull the object upwards. (weight of A is greater than 170 N)
So, a1= 0 m/s²
Force acting on B in upward direction is 170 N and weight is 10g or 100 N. Net force in upward direction is 70 N. so,
a2= 7 m/s²
A painter is raising himself and the crate on which he stands with an acceleration of 5m/s² by a massless rope–and–pulley arrangement. Mass of painter is 100 kg and that of the crate is 50 kg. If g = 10 m/s², then :
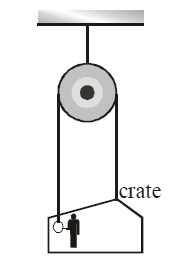

Let us assume tension force in the wire is T. Then net force acting on man and crate in upward direction is 2T. Gravitational force acting in downward direction is (50+100) g = 1500 N. Writing equation of motion for the system.
2T- 1500 = 150 × a
⇒ 2T- 1500 = 150 × 5
⇒ 2T = 750 +1500 = 2250
⇒ T = 1125 N
The block A is moving downward with constant velocity v0. Find the velocity of the block B, when the string makes an angle θ with the horizontal.
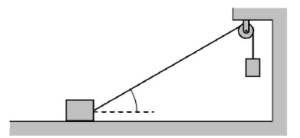
When two objects are connected by a string component of velocity along the string remains equal.
v1 cosθ = v 0
⇒v1= v0/ cosθ
The force F needed to keep the block at equilibrium in given figure is (pulley and string are massless)
In the arrangement, shown in figure, pulleys A and B are massless and frictionless and threads are ideal. Block of mass m1 will remain at rest if:
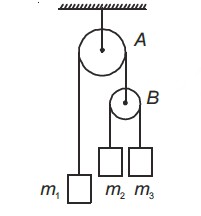

In the movable pulley system, tension in the string connecting m2 and m3 is:
Since this tension acts twice to balance
, we equate:
Cancelling
and rearranging gives:
If acceleration of block m1 is a downward then acceleration of block m2 will be:
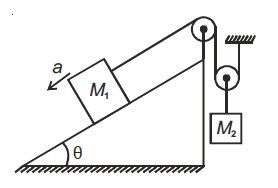
For ideal pulleys, the product of tension and acceleration remains constant:
Since , substitute to get:
What is the minimum value of F needed so that block begins to move upward on frictionless incline plane as shown?
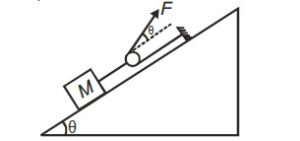
Total upward force along incline =
Downward component of weight =
Now use the identity: