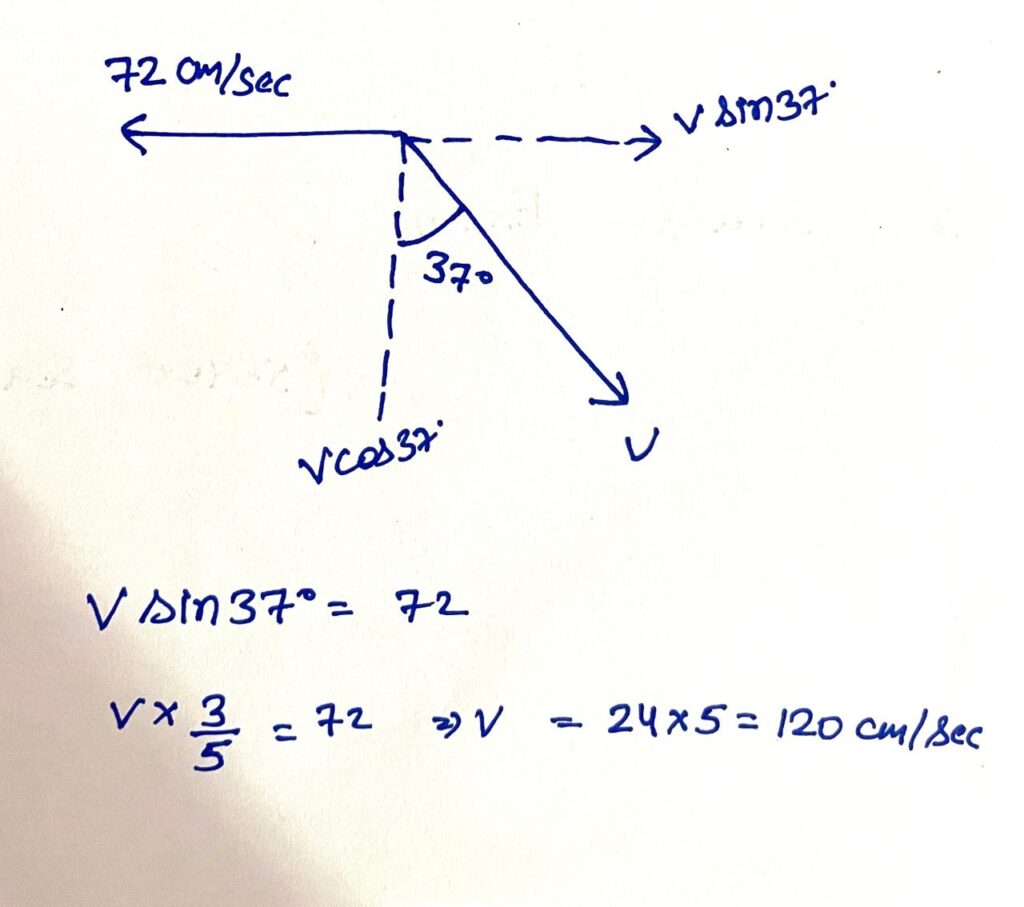
A man walks in rain at 72 cm/s due east and observes the rain falling vertically. When he stops, rain appears to strikes his back at 37º from the vertical. Find velocity of raindrops relative to the ground.
Relative Motion in Two Dimension
A man wishes to swim across a river 400 m wide flowing with a speed of 3m/s, such that he reaches the point just in front on the other bank in time not greater than 100 sec. The angle made by the direction he swims and river flow direction is :
Solution:
Distance travelled in y-direction = 400 m
Time to cross = 100 sec
So, Speed in y-direction = 4 m/s
Speed in x-direction = 3m/s
So, angle = 90 +37 =127º
Rain drops are falling vertically and a man is running on the ground horizontally with speed equal to the rain with respect to the ground. Rain drops appears to him hitting with velocity 10 km/hr. Find velocity of rain.
Solution:
Velocity of Rain = - V j
Velocity of Person = V i
Velocity of Rain with respect to the Person = - V i - V j
so, V√2 = 10 ⇒ V = 5√2 km/hr
A river flows from east to west with a speed of 5m/min. A man on south bank of river, capable of swimming at the rate of 10 m/min in still water, wants to swim across the river in shortest time; he should swim :
Solution:
To cross the river in the shortest time, the man should swim directly perpendicular to the riverbank, regardless of the river's flow. This way, his entire swimming speed is used to cross the river.
Given:
- Speed of the river (east to west) = 5 m/min
- Speed of the swimmer in still water = 10 m/min
The swimmer should aim **directly north** to minimize the crossing time. The river's current will cause him to drift downstream, but this direction ensures the shortest crossing time.
Thus, the man should swim:
\[
{\text{directly north}}
\]
A river is flowing at the rate of 6 km/h. A swimmer swims across the river with a velocity of 9 km/h w.r.t. water. The resultant velocity of the man will be in (km/h) :
Solution:
The resultant velocity of the swimmer is the vector sum of the river's velocity and the swimmer's velocity relative to the water.
Given:
- River velocity = 6 km/h
- Swimmer's velocity relative to water = 9 km/h
Using the Pythagorean theorem:
\[
v_{\text{resultant}} = \sqrt{(9^2 + 6^2)} = \sqrt{81 + 36} = \sqrt{117}
\]
Thus, the resultant velocity of the swimmer is:
\[
{\sqrt{117} \text{km/h}}
\]
A man wishes to swim across a river 0.5 km wide. If he can swim at the rate of 2 km/h in still water and the river flows at the rate of 1 km/h. The angle made by the directon (w.r.t. the flow of the river) along which he should swim so as to reach a point exactly opposite his starting point, should be :
Solution:
To swim across the river and reach a point directly opposite his starting point, the man must swim at an angle against the flow of the river to counteract the river's current.
### Given:
- Speed of the man in still water = 2 km/h
- Speed of the river flow = 1 km/h
Let \(\theta\) be the angle between the man's swimming direction and the river flow. To counteract the river's flow, the horizontal component of the man's velocity must equal the river's velocity.
\[
\text{Horizontal component} = 2 \sin \theta = 1
\]
Solving for \(\theta\):
\[
\sin \theta = \frac{1}{2}
\]
\[
\theta = \sin^{-1} \left( \frac{1}{2} \right) = 30^\circ
\]
Thus, the man should swim at an angle of:
\[
{120^\circ} \text{ upstream from the river flow.}
\]
A boat-man can row a boat to make it move with a speed of 10 km/h in still water. River flows steadily at the rate of 5 km/h. and the width of the river is 2 km. If the boat man cross the river along the minimum distance of approach then time elapsed in rowing the boat will be :
Solution:
To cross the river along the minimum distance (i.e., directly perpendicular to the riverbank), the boatman must row with a velocity component equal and opposite to the river flow to cancel the drift.
Given:
- Speed of the boat in still water = 10 km/h
- Speed of the river flow = 5 km/h
- Width of the river = 2 km
The boat's velocity perpendicular to the riverbank is:
\[
v_{\text{perpendicular}} = \sqrt{(10^2 - 5^2)} = \sqrt{100 - 25} = \sqrt{75} = 5\sqrt{3} \, \text{km/h}
\]
Time to cross the river:
\[
\text{Time} = \frac{\text{Distance}}{\text{Speed perpendicular}} = \frac{2}{5\sqrt{3}} \, \text{hours}
\]
Simplifying:
\[{\frac{2}{5\sqrt{3}} \, \text{hours}}
\]
A bird is flying towards south with a velocity 40km/h and a train is moving with a velocity 40 km/h towards east. What is the velocity of the bird w.r.t. an observer in the train ?
Solution:
The relative velocity of the bird with respect to the observer in the train is found by combining the bird's velocity (south) and the train's velocity (east) using the Pythagorean theorem.
\[
v_{\text{relative}} = \sqrt{(40^2 + 40^2)} = \sqrt{3200} = 40\sqrt{2} \, \text{km/h}
\]
The direction is \( 45^\circ \) south of west.
Thus, the relative velocity is:
\[ {40\sqrt{2} \, \text{km/h} \text{ at } 45^\circ \text{ south of west}}
\]
A train moves in north direction with a speed of 54 km/h A monkey is running on the roof of the train, against its motion with a velocity of 18 km/h. with respect to train. The velocity of monkey as observed by a man standing on the ground is :
Solution:
To find the velocity of the monkey as observed by a man standing on the ground, we need to add the velocity of the monkey relative to the train to the velocity of the train.
Given:
- Velocity of the train (north direction) = 54 km/h
- Velocity of the monkey relative to the train (opposite to train's motion) = 18 km/h
Monkey's velocity relative to the ground:
Since the monkey is running against the train’s motion, the monkey's velocity relative to the ground will be:
\[
\vec{v}_{\text{monkey}} = \vec{v}_{\text{train}} - \vec{v}_{\text{monkey relative to train}}
\]
\[
v_{\text{monkey}} = 54 \, \text{km/h} - 18 \, \text{km/h} = 36 \, \text{km/h}
\]
Thus, the velocity of the monkey as observed by a man on the ground is:
\[
{36 \, \text{km/h} \text{ north} or 10 m/s \text{ north}}
\]
A boy is running on a levelled road with velocity (v) with a long hollow tube in his hand. Water is falling vertically downwards with velocity (u). At what angle to the vertical, should he incline the tube so that the water drops enters without touching its side :
Solution:
The tube should be inclined at an angle \(\theta\) such that the water's relative velocity to the boy is along the axis of the tube.
The horizontal velocity of the boy is \(v\), and the vertical velocity of the falling water is \(u\). The angle \(\theta\) between the tube and the vertical satisfies:
\[
\tan \theta = \frac{v}{u}
\]
Thus, the required angle is:
\[
\theta = \tan^{-1} \left( \frac{v}{u} \right)
\]