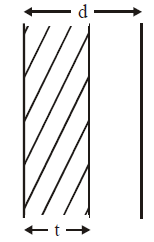
Question 8: A parallel plate capacitor with air between the plates has a capacitance of 9 pF. The separation between its plates is ‘d’. The space between the plates is now filled with two dielectrics. One of the dielectrics has dielectric constant k1 = 3 and thickness d/3 while the other one has dielectric constant k2 = 6 and thickness 2d/3. Capacitance of the capacitor is now :
View Solution
Solution:
Given:
- Initial capacitance with air as the dielectric:
- Dielectric constants: ,
- Thicknesses of the dielectrics: and
Step-by-step solution:
1. Capacitance formula:
The capacitance of a parallel plate capacitor is:
Where:
- is the dielectric constant,
- is the permittivity of free space,
- is the area of the plates,
- is the separation between the plates.
When we insert dielectrics in series, we treat the system as two capacitors in series with different dielectric constants.
2. Capacitance of each section:
- For the dielectric with and thickness , the capacitance is:
- For the dielectric with and thickness , the capacitance is:
3. Total capacitance:
The total capacitance of the system is found by treating the two capacitances in series. For capacitors in series, the total capacitance is given by:
Substitute :
Thus,
4. Relating to the original capacitance:
The original capacitance with air as the dielectric is:
Therefore, the total capacitance becomes:
Final Answer:
The total capacitance with the two dielectrics is 40.5 pF.
Thus, 40.5 pF is the correct answer.
Discuss this question