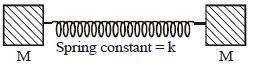
Solution:

The system shown consists of two masses \( M \) connected by a spring with a spring constant \( k \). Since the masses are identical, the angular frequency \( \omega \) of the system for oscillations is given by:

\[
\omega = \sqrt{\frac{k}{\text{reduced mass}}}
\]

In this case, the reduced mass \( \mu \) of the system is given by:

\[
\mu = \frac{M \cdot M}{M + M} = \frac{M}{2}
\]

Thus, the angular frequency \( \omega \) is:

\[
\omega = \sqrt{\frac{k}{M/2}} = \sqrt{\frac{2k}{M}}
\]

Answer:

\[
\omega = \sqrt{\frac{2k}{M}}
\]