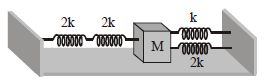
Solution:

1. Left Side:
- Two springs with spring constants \( 2k \) and \( 2k \) are in series.
- The combined spring constant \( k_{\text{left}} \) for these two springs in series is:
\[
\frac{1}{k_{\text{left}}} = \frac{1}{2k} + \frac{1}{2k} = \frac{1}{k}
\]
\[
k_{\text{left}} = k
\]

2. Right Side:
- Two springs with spring constants \( k \) and \( 2k \) are in parallel.
- The combined spring constant \( k_{\text{right}} \) for these two springs in parallel is:
\[
k_{\text{right}} = k + 2k = 3k
\]

3. Combine Left and Right Sides:
- Since \( k_{\text{left}} \) and \( k_{\text{right}} \) are in parallel, the equivalent spring constant \( k_{\text{eq}} \) is:
\[
k_{\text{eq}} = k_{\text{left}} + k_{\text{right}} = k + 3k = 4k
\]

Step 2: Calculate the Frequency of Oscillation

The frequency \( f \) is given by:

\[
f = \frac{1}{2\pi} \sqrt{\frac{k_{\text{eq}}}{M}}
\]

Substitute \( k_{\text{eq}} = 4k \):

\[
f = \frac{1}{2\pi} \sqrt{\frac{4k}{M}}
\]

Final Answer

\[
f = \frac{1}{2\pi} \sqrt{\frac{4k}{M}}
\]