NEET Physics Question - Laws of Motion

In the arrangement, shown in figure, pulleys A and B are massless and frictionless and threads are ideal. Block of mass m1 will remain at rest if: Image related to

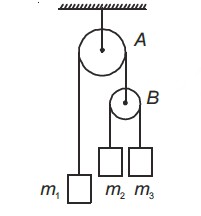
\[ \frac{1}{m_{3}}=\frac{2}{m_{2}}+\frac{3}{m_{1}} \]

\[ m_{1}= m_{2}= m_{3} \]

\[ \frac{4}{m_{1}}=\frac{1}{m_{2}}+\frac{1}{m_{3}}\]

\[ \frac{1}{m_{1}}=\frac{1}{m_{2}}+\frac{1}{m_{3}}\]

Solution:

nlm constrained motion

In the movable pulley system, tension in the string connecting m2 and m3 is:

$T = \frac{2 m_2 m_3 g}{m_2 + m_3}$

Since this tension acts twice to balance

$m_1$

, we equate:

$2T = m_1 g \Rightarrow \frac{4 m_2 m_3 g}{m_2 + m_3} = m_1 g$

Cancelling

$g$

and rearranging gives:

$\boxed{ \frac{4}{m_{1}} = \frac{1}{m_{2}} + \frac{1}{m_{3}} }$

Rankers Physics

Solution:

Leave a Reply Cancel reply