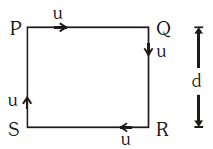
Solution:

To determine when the four persons \( P, Q, R, \) and \( S \) will meet, consider the following:

Relative Velocity:
- Each person moves with speed \( u \) towards the center of the square.

Configuration:
- As they face each other and move towards the center, their paths converge.

Effective Speed Towards Each Other:
- The effective speed of each person towards the center is \( u \cos 45^\circ = \frac{u}{\sqrt{2}} \) because they move diagonally.

Distance to Center:
- The distance from each person to the center of the square is \( \frac{d}{\sqrt{2}} \).

Time to Meet:
\[
t = \frac{\text{Distance}}{\text{Effective Speed}} = \frac{\frac{d}{\sqrt{2}}}{\frac{u}{\sqrt{2}}} = \frac{d}{u}
\]

Thus, the time after which they will all meet is \( \frac{d}{u} \).