Solution:
The additional kinetic energy required to transfer a satellite from a circular orbit of radius \( R_1 \) to \( R_2 \) is the difference in kinetic energy between the two orbits.
Kinetic energy in a circular orbit is:
\[
K = \frac{GMm}{2R}
\]
The kinetic energy difference is:
\[
\Delta K = \frac{GMm}{2R_1} - \frac{GMm}{2R_2}
\]
Simplifying:
\[
\Delta K = \frac{GMm}{2} \left( \frac{1}{R_1} - \frac{1}{R_2} \right)
\]
So, the additional kinetic energy is:
\[
\Delta K = \frac{GMm}{2} \left( \frac{1}{R_1} - \frac{1}{R_2} \right)
\]
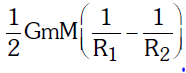
Leave a Reply