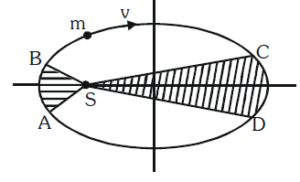
Solution:
According to **Kepler's second law** (law of areas), a planet sweeps out equal areas in equal times. This means the area swept out is proportional to the time taken.
In the problem, the area \( SCD \) is given to be twice the area \( SAB \). Therefore, the time taken to sweep these areas will also follow the same ratio.
Thus, the relation between the times is:
\[
t_1 = 2 t_2
\]
So, the time taken to move from \( C \) to \( D \) is twice the time taken to move from \( A \) to \( B \).
Leave a Reply