Solution:
The orbital velocity \( v \) at a height \( h \) above the Earth's surface is given by:
\[
v = \sqrt{\frac{GM}{R + h}}
\]
For the satellite orbiting just above the Earth's surface (i.e., \( h = 0 \)), the velocity is:
\[
v_0 = \sqrt{\frac{GM}{R}}
\]
For a satellite at an altitude of \( h = \frac{R}{2} \), the velocity \( v_h \) becomes:
\[
v_h = \sqrt{\frac{GM}{R + \frac{R}{2}}} = \sqrt{\frac{GM}{\frac{3R}{2}}} = \sqrt{\frac{2}{3}} v_0
\]
Thus, the orbital velocity at an altitude of \( \frac{R}{2} \) is:
\[
v_h = \sqrt{\frac{2}{3}} v_0
\]
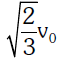
Leave a Reply