Solution:
When both \( r_1 \) and \( r_2 \) are greater than \( R \) (i.e., both are outside the sphere), the gravitational force at a distance \( r \) from the center of a uniform sphere is given by:
\[
F = \frac{G M}{r^2}
\]
So, the forces \( F_1 \) and \( F_2 \) at distances \( r_1 \) and \( r_2 \) from the center are:
\[
F_1 = \frac{G M}{r_1^2}
\]
\[
F_2 = \frac{G M}{r_2^2}
\]
Now, taking the ratio \( \frac{F_1}{F_2} \):
\[
\frac{F_1}{F_2} = \frac{\frac{G M}{r_1^2}}{\frac{G M}{r_2^2}} = \frac{r_2^2}{r_1^2}
\]
Thus, the ratio of the gravitational forces is:
\[
\frac{F_1}{F_2} = \left( \frac{r_2}{r_1} \right)^2
\]
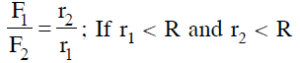
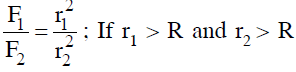
Leave a Reply