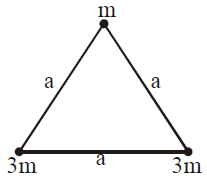
Solution:

To find the net gravitational force on the mass \( m \) at the centroid, we follow these steps:

1. Forces due to extra masses \( 2m \):
- Each of the two lower vertices has an extra mass \( 2m \).
- The gravitational force due to one \( 2m \) mass at a distance \( \frac{a}{\sqrt{3}} \) from the centroid is:
\[
F = \frac{G (2m) m}{\left( \frac{a}{\sqrt{3}} \right)^2} = \frac{6 G m^2}{a^2}
\]

2. Net force between the two extra masses:
- The angle between the two forces is \( 120^\circ \).
- The resultant force is given by the vector addition formula:
\[
F_{\text{resultant}} = \sqrt{F^2 + F^2 + 2 F F \cos 120^\circ}
\]
Since \( \cos 120^\circ = -\frac{1}{2} \):
\[
F_{\text{resultant}} = \sqrt{F^2 + F^2 - F^2} = F = \frac{6 G m^2}{a^2}
\]

3. Conclusion:
The net gravitational force on the mass \( m \) at the centroid is:
\[
F_{\text{resultant}} = \frac{6 G m^2}{a^2}
\]
This force is directed vertically downward.