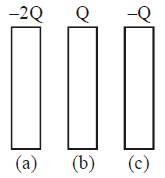
Solution:

Yes, direct formulas can simplify the solution for problems like this involving conducting plates. Here's how:

Formula for charge redistribution in conductors:
For three parallel conducting plates with charges \( Q_1, Q_2, Q_3 \):
1. The charge on the inner faces is:
\[
Q_{\text{inner}} = \frac{Q_1 - Q_3}{2}
\]
2. The charge on the  outer faces remains equal to the net charge on the respective plates:
- Outer left face: \( Q_1 \)
- Outer right face: \( Q_3 \)

---

Applying the formula:
- Given charges:
\[
Q_1 = -2Q, \, Q_2 = Q, \, Q_3 = -Q
\]
- Charge on the inner faces of plate \( b \):
\[
Q_{\text{inner}} = \frac{Q_1 - Q_3}{2} = \frac{-2Q - (-Q)}{2} = \frac{-2Q + Q}{2} = \frac{-Q}{2}
\]

- Since the **right face of \( b \)** contributes to the inner faces:
\[
Q_{\text{right face of \( b \)}} = 0
\]

Final Answer:
\[
{Zero (0)}
\]