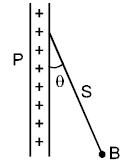
Solution:

To solve for the proportionality of the surface charge density \(\sigma\) with \(\tan\theta\), we analyze the forces acting on the charged ball \(B\):

Step 1: Forces acting on the ball
1. Gravitational force (\(F_g\)): Acts vertically downward, magnitude \(F_g = mg\), where \(m\) is the mass of the ball.
2. Electric force (\(F_e\)): Acts horizontally, due to the electric field produced by the charged conducting sheet.
3. Tension (\(T\)): Acts along the silk thread, balancing the net forces in both horizontal and vertical directions.

The electric field near a charged conducting sheet with surface charge density \(\sigma\) is:

\[
E = \frac{\sigma}{2\epsilon_0}
\]

The electric force on the ball is:

\[
F_e = qE = q \cdot \frac{\sigma}{2\epsilon_0}
\]

Step 2: Force balance
At equilibrium:
- In the vertical direction: \(T \cos\theta = mg\)
- In the horizontal direction: \(T \sin\theta = F_e = q \cdot \frac{\sigma}{2\epsilon_0}\)

Taking the ratio of the horizontal and vertical components:

\[
\tan\theta = \frac{T \sin\theta}{T \cos\theta} = \frac{F_e}{F_g} = \frac{q \cdot \frac{\sigma}{2\epsilon_0}}{mg}
\]

\[
\tan\theta \propto \sigma
\]

Final Answer:
The surface charge density \(\sigma\) of the sheet is proportional to:

\[
{\tan\theta}
\]