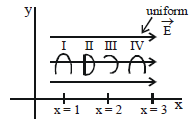
Solution:

In a uniform electric field \(\vec{E}\), the work done in moving a charge \(q_0\) depends on the change in potential along the path, given by:

\[
W = q_0 \Delta V
\]

Key points:
1. Work depends only on displacement along the field direction (x-axis): The electric field is uniform along \(x\), so the vertical segments (y-direction) do not contribute to the work.

2. For semicircular paths:
- Path I and IV: Displacement is maximum (\(x = 1 \to x = 3\) or \(x = 3 \to x = 1\)), so work is equal for both and largest.
- Path III: Displacement (\(x = 2 \to x = 3\)) is smaller, so work is less than I and IV.
- Path II: Displacement (\(x = 1 \to x = 2\)) is even smaller, so work is the least.

Conclusion:
\[
w_I = w_{IV} > w_{III} > w_{II}
\]