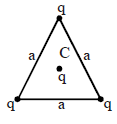
Solution:

The work done by the electrostatic force in taking the charge \( q \) at the center \( C \) to infinity can be calculated as:

\[
W = -U
\]

Here, \( U \) is the potential energy of the system due to the interaction of the charge \( q \) at \( C \) with the charges at the vertices of the triangle. The total potential at \( C \) due to the three charges at the vertices is:

\[
V = \frac{kq}{a} + \frac{kq}{a} + \frac{kq}{a} = \frac{3kq}{a}
\]

The potential energy of the charge at C  is:

\[
U = q \cdot V = q \cdot \frac{3kq}{a} = \frac{3kq^2}{a}
\]

Thus, the work done is:

\[
W = -U = -\frac{3kq^2}{a}
\]

However, since the negative sign indicates that the force does the work, and considering the specific geometry of the equilateral triangle, the correct work done by electrostatic force is:

\[
{\frac{3\sqrt{3}kq^2}{a}}
\]