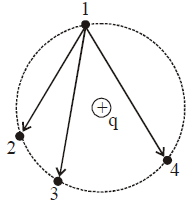
Solution:

Explanation and Solution

The work done by an electrostatic field in moving a charge from one point to another depends only on the electric potential difference between the two points, since the electrostatic force is conservative.

---

Given:
- We have a point charge \(q\) at the center of a circle.
- Points 1, 2, 3, and 4 lie on the same circle around the charge \(q\).

Step 1: Understand the electric potential
The electric potential \(V\) at any point on a circle centered around the charge \(q\) is the same because:

\[
V = \frac{kq}{r}
\]

where \(r\) is the radius of the circle. Since points 1, 2, 3, and 4 are equidistant from \(q\), the potential at all these points is identical.

---

Step 2: Work done in moving a charge
The work done \(W\) in moving a charge \(Q\) from one point to another in an electrostatic field is given by:

\[
W = Q (V_{\text{final}} - V_{\text{initial}})
\]

Since the potential \(V\) is the same at points 2, 3, and 4, the potential difference for each movement is zero:

\[
V_{\text{final}} = V_{\text{initial}}
\]

Thus, for movements from point 1 to points 2, 3, and 4, the work done:

\[
W_2 = W_3 = W_4 = 0
\]

---

Final Comparison:
The work done \(W_2\), \(W_3\), and \(W_4\) are all equal. Hence:

\[
{W_2 = W_3 = W_4 = 0}
\]

This result arises because the electric field is conservative and the movement is along an equipotential surface.