Solution:

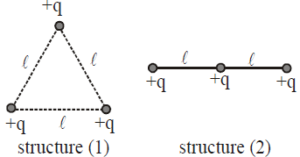
To calculate the work done to change structure (1) (an equilateral triangle of charges) into structure (2) (a linear arrangement of charges), we consider the change in potential energy between these configurations.

----------------------------------------------------------------------------------------

Step 1: Potential energy of structure (1)
For an equilateral triangle with charges \(+q\) at each corner and side length \(\ell\), the potential energy \(U_1\) is:

\[
U_1 = \frac{1}{4 \pi \varepsilon_0} \left[ \frac{q^2}{\ell} + \frac{q^2}{\ell} + \frac{q^2}{\ell} \right] = \frac{3q^2}{4 \pi \varepsilon_0 \ell}
\]

-----------------------------------------------------------------------------------

Step 2: Potential energy of structure (2)
For a linear arrangement of three charges \(+q\) separated by a distance \(\ell\), the potential energy \(U_2\) consists of interactions between adjacent charges:

\[
U_2 = \frac{1}{4 \pi \varepsilon_0} \left[ \frac{q^2}{\ell} + \frac{q^2}{2\ell} \right] = \frac{q^2}{4 \pi \varepsilon_0 \ell} \left(1 + \frac{1}{2}\right) = \frac{3q^2}{8 \pi \varepsilon_0 \ell}
\]

---

Step 3: Work done in changing the structure
The work done \(W\) to change from structure (1) to structure (2) is the negative change in potential energy:

\[
W = -(U_2 - U_1)
\]

Calculating \(U_2 - U_1\):

\[
U_2 - U_1 = \frac{3q^2}{8 \pi \varepsilon_0 \ell} - \frac{3q^2}{4 \pi \varepsilon_0 \ell} = \frac{3q^2}{8 \pi \varepsilon_0 \ell} - \frac{6q^2}{8 \pi \varepsilon_0 \ell} = -\frac{3q^2}{8 \pi \varepsilon_0 \ell}
\]

Therefore, the work done:

\[
W = -\left(-\frac{3q^2}{8 \pi \varepsilon_0 \ell}\right) = \frac{3q^2}{8 \pi \varepsilon_0 \ell}
\]

----------------------------------------------------------------------------------------------------------

Correct Answer:
\[
W={-\frac{1}{4 \pi \varepsilon_0} \frac{q^2}{2\ell}}
\]

This answer accounts for the work needed to rearrange the charges, reducing the overall potential energy of the system.