Solution:

The electric flux \(\Phi\) through the Gaussian surface can be found using Gauss's law:

\[
\Phi = \frac{q_{\text{enc}}}{\epsilon_0}
\]

Here, \(q_{\text{enc}}\) is the charge enclosed by the spherical Gaussian surface.

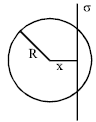
Since the infinite sheet has a uniform surface charge density \(\sigma\), the charge enclosed is the product of \(\sigma\) and the area of the sheet that lies inside the sphere. The area of the sheet within the sphere is the area of the circle formed by the intersection, which has a radius \(r\) determined by the geometry of the sphere and the plane.

1. The radius of the intersection circle is \(r = \sqrt{R^2 - x^2}\).
2. The area of this circle is \(A = \pi r^2 = \pi (R^2 - x^2)\).

Thus, the enclosed charge is:

\[
q_{\text{enc}} = \sigma A = \sigma \pi (R^2 - x^2).
\]

Substituting this into Gauss's law:

\[
\Phi = \frac{\sigma \pi (R^2 - x^2)}{\epsilon_0}.
\]

So, the electric flux through the Gaussian surface is:

\[
\Phi = \frac{\sigma \pi (R^2 - x^2)}{\epsilon_0}.
\]