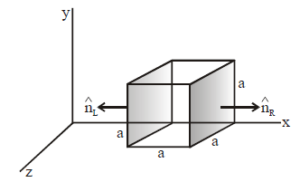
Solution:

We are tasked with finding the charge enclosed within the cube using Gauss's Law:

\[
\Phi_{\text{net}} = \frac{q_{\text{enc}}}{\varepsilon_0}.
\]

Given:
- Net flux through the cube: \(\Phi_{\text{net}} = 1.05 \, \text{Nm}^2\text{C}^{-1}\),
- \(\varepsilon_0 = 8.85 \times 10^{-12} \, \text{C}^2\text{N}^{-1}\text{m}^{-2}\),
- \(\alpha = 800 \, \text{N}\text{C}^{-1}\text{m}^{-1/2}\),
- Cube side length: \(a = 0.1 \, \text{m}\).

Steps:

1. Use Gauss's Law:
The enclosed charge \(q_{\text{enc}}\) is related to the flux by:
\[
q_{\text{enc}} = \varepsilon_0 \Phi_{\text{net}}.
\]

2. Substitute the values:
\[
q_{\text{enc}} = (8.85 \times 10^{-12}) \cdot (1.05).
\]

3. Calculate:
\[
q_{\text{enc}} = 9.27 \times 10^{-12} \, \text{C}.
\]

Final Answer:
The enclosed charge is:
\[
{9.27 \times 10^{-12} \, \text{C}}.
\]