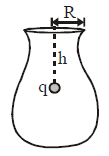
Solution:

To calculate the electric flux through the lateral surface of the vessel, we apply Gauss's law and consider the symmetry of the system.

---=====================================

Step-by-Step Solution:

1. Total Flux from the Charge \(q\):
The total flux emitted by the point charge \(q\) in all directions is:
\[
\Phi_{\text{total}} = \frac{q}{\varepsilon_0}.
\]

2. Flux Through the Circular Mouth:
Using the geometry of the vessel, the charge \(q\) is placed at a depth \(h = \sqrt{3}R\). The flux through the circular mouth of radius \(R\) can be calculated as:
\[
\Phi_{\text{mouth}} = \frac{q}{2\varepsilon_0}.
\]

3. Flux Through the Lateral Surface
By symmetry, the flux through the lateral surface is the remaining flux from the total flux after subtracting the flux through the mouth:
\[
\Phi_{\text{lateral}} = \Phi_{\text{total}} - \Phi_{\text{mouth}}.
\]

4. Simplify:
Substitute the values:
\[
\Phi_{\text{lateral}} = \frac{q}{\varepsilon_0} - \frac{q}{2\varepsilon_0}.
\]
\[
\Phi_{\text{lateral}} = \frac{q}{2\varepsilon_0} \left(1 + \frac{\sqrt{3}}{2}\right).
\]

----------------------------------------------------------------------------------------

Final Answer:
The electric flux through the lateral surface of the vessel is:
\[
{\frac{q}{2\varepsilon_0} \left( 1 + \frac{\sqrt{3}}{2} \right)}.
\]