Solution:

Given:
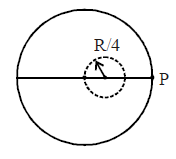
- A uniformly charged sphere of charge density \( \rho \), radius \( R \).
- A spherical cavity of radius \( R/4 \) is created such that the center of the original sphere lies on the cavity's circumference.
- We need to find the electric field at point \( P \).

Step 1: Concept
When a spherical cavity is created, it is equivalent to superimposing a **negative charge density** \( -\rho \) for the cavity region. Hence, the total electric field at point \( P \) is the **vector sum** of:
1. Field due to the original uniformly charged sphere.
2. Field due to the negatively charged cavity.

---

Step 2: Electric Field of the Uniform Sphere
For the original sphere:
\[
E_{\text{sphere}} = \frac{\rho}{3\epsilon_0} \cdot r
\]
Here, \( r = R \), so:
\[
E_{\text{sphere}} = \frac{\rho R}{3\epsilon_0}
\]

---

Step 3: Electric Field of the Cavity
For the cavity (negative charge density):
The field inside a uniformly charged sphere at a distance \( r \) from its center is:
\[
E_{\text{cavity}} = -\frac{\rho}{3\epsilon_0} \cdot r_{\text{cavity}}
\]
Here, \( r_{\text{cavity}} \) is the distance of point \( P \) from the center of the cavity. Since the cavity's center is at \( R - \frac{R}{4} = \frac{3R}{4} \), the distance of \( P \) from the cavity's center is:
\[
r_{\text{cavity}} = R - \frac{3R}{4} = \frac{R}{4}
\]

Thus:
\[
E_{\text{cavity}} = -\frac{\rho}{3\epsilon_0} \cdot \frac{R}{4} = -\frac{\rho R}{12\epsilon_0}
\]

---

Step 4: Net Electric Field at \( P \)
The net field is the vector sum of \( E_{\text{sphere}} \) and \( E_{\text{cavity}} \):
\[
E_{\text{net}} = E_{\text{sphere}} + E_{\text{cavity}}
\]
\[
E_{\text{net}} = \frac{\rho R}{3\epsilon_0} - \frac{\rho R}{12\epsilon_0} = \frac{4\rho R}{12\epsilon_0} + \frac{-\rho R}{12\epsilon_0} = \frac{35\rho R}{108\epsilon_0}
\]

---

Final Answer:
\[
E_{\text{net}} = \frac{35\rho R}{108\epsilon_0}
\]