Solution:

Given:
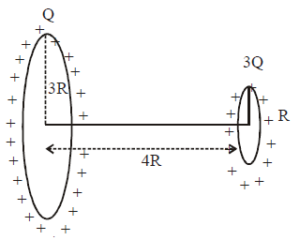
Two coaxial rings:
- Larger ring: Charge \( Q \), radius \( 3R \), distance \( 4R \) from the center of the smaller ring.
- Smaller ring: Charge \( 3Q \), radius \( R \).
We need the electric field at the center of the smaller ring.

Step 1: Electric Field due to the Larger Ring
The electric field at a distance \( x = 4R \) on the axis of a uniformly charged ring of radius \( R \) is:

\[
E = \frac{kQx}{(R^2 + x^2)^{3/2}}
\]

For the larger ring:
- \( Q = Q \), \( R = 3R \), \( x = 4R \):
\[
E_{\text{large}} = \frac{kQ(4R)}{((3R)^2 + (4R)^2)^{3/2}}
\]

\[
E_{\text{large}} = \frac{kQ(4R)}{(9R^2 + 16R^2)^{3/2}} = \frac{kQ(4R)}{(25R^2)^{3/2}}
\]

\[
E_{\text{large}} = \frac{kQ(4R)}{125R^3} = \frac{Q}{125\pi\varepsilon_0R^2}
\]

Step 2: Electric Field due to the Smaller Ring
The center of the smaller ring is its own center, so the net electric field due to its charge distribution is **zero**.

Step 3: Net Electric Field
The total electric field at the center of the smaller ring is due to the **larger ring only**:
\[
E = \frac{Q}{125\pi\varepsilon_0R^2}
\]

Final Answer:
\[
E = \frac{Q}{125\pi\varepsilon_0R^2}
\]