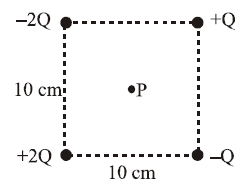
Solution:

Explanation:

To determine the direction of the electric field at the center \(P\), we consider the contributions of the electric fields due to each charge:

1. Electric Field Due to Each Charge:
- The electric field at point \(P\) due to a charge at a corner of the square points away from the charge if it is positive, and toward the charge if it is negative.

2. Symmetry of the Problem:
- Opposite charges on diagonally opposite corners will partially cancel their contributions due to symmetry in their horizontal (\(x\)) or vertical (\(y\)) components.
- However, due to the **asymmetry in the magnitudes of the charges**, there will be a net resultant field.

3. Analyzing the Contributions:
- The charge \(-2Q\) (top left) will produce a stronger electric field toward itself compared to \(+Q\) (top right).
- Similarly, the charge \(+2Q\) (bottom left) will produce a stronger field away from itself compared to \(-Q\) (bottom right).
- The vertical components of the fields due to the charges \(-2Q\) and \(+2Q\) add **upward**.
- The horizontal components of the fields due to opposite charges (\(-2Q\) and \(+2Q\), and \(+Q\) and \(-Q\)) cancel each other.

4. Result:
- The net electric field at point \(P\) is directed upward, dominated by the vertical components due to the unequal magnitudes of the charges.

Hence, the correct answer is upward.