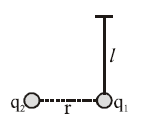
Solution:

Solution Outline:

1. Forces Acting on \( q_1 \):
- Gravitational Force: \( F_g = mg \), acting vertically downward.
- Electrostatic Force: \( F_e = \frac{k |q_1 q_2|}{r^2} \), acting horizontally toward \( q_2 \).

2. Resultant Tension \( T \)
Since \( q_1 \) is in equilibrium, the tension \( T \) in the thread must balance both the gravitational and electrostatic forces. The tension will act diagonally, with components to counteract both the vertical \( mg \) and horizontal \( F_e \) forces.

3. Calculating \( T \):
Using vector addition, we find \( T \) as:
\[
T = \sqrt{(mg)^2 + \left( \frac{k |q_1 q_2|}{r^2} \right)^2}
\]

Since \( \frac{k |q_1 q_2|}{r^2} \) is a positive quantity, \( T \) is indeed greater than \( mg \).

Conclusion:
The correct answer is:
\[
T > mg
\]