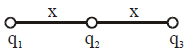
Solution:

To find the relation between \( q_1 \) and \( q_2 \) for \( q_3 \) to be in equilibrium, let's analyze the forces on \( q_3 \).

1. Forces on \( q_3 \):
- The force due to \( q_1 \) on \( q_3 \) is:
\[
F_{13} = \frac{k |q_1| |q_3|}{(2x)^2} = \frac{k |q_1| |q_3|}{4x^2}
\]
(directed towards \( q_1 \) if \( q_1 \) and \( q_3 \) have opposite signs).

- The force due to \( q_2 \) on \( q_3 \) is:
\[
F_{23} = \frac{k |q_2| |q_3|}{x^2}
\]
(directed towards \( q_2 \) if \( q_2 \) and \( q_3 \) have opposite signs).

2. Equilibrium Condition for \( q_3 \):
For \( q_3 \) to be in equilibrium, these forces must be equal in magnitude:
\[
F_{13} = F_{23}
\]
Substituting the values:
\[
\frac{k |q_1| |q_3|}{4x^2} = \frac{k |q_2| |q_3|}{x^2}
\]
Cancelling \( k \), \( |q_3| \), and \( x^2 \) from both sides, we get:
\[
\frac{|q_1|}{4} = |q_2|
\]
Therefore:
\[
q_1 = -4q_2
\]

Answer:
The relation between \( q_1 \) and \( q_2 \) is:
\[
q_1 = -4q_2
\]