Solution:

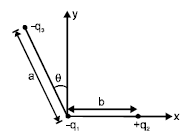
To find the \( x \)-component of the force on charge \(-q_1\) in the given setup, let's break down the forces due to \( +q_2 \) and \( -q_3 \) on \( -q_1 \).

1. Force due to \( +q_2 \):
The force \( F_{12} \) between \( -q_1 \) and \( +q_2 \) acts along the \( x \)-axis (horizontally) and has a magnitude:
\[
F_{12} = \frac{k |q_1| |q_2|}{b^2}
\]
Since this force acts along the positive \( x \)-direction, the \( x \)-component of this force is simply:
\[
F_{12x} = \frac{k |q_1| q_2}{b^2}
\]

2. Force due to \( -q_3 \):
The force \( F_{13} \) between \( -q_1 \) and \( -q_3 \) acts along the line joining them, which makes an angle \( \theta \) with the \( y \)-axis. The magnitude of this force is:
\[
F_{13} = \frac{k |q_1| |q_3|}{a^2}
\]
To find the \( x \)-component of \( F_{13} \), we use the angle \( \theta \) with the \( y \)-axis. The \( x \)-component of \( F_{13} \) is:
\[
F_{13x} = \frac{k |q_1| |q_3|}{a^2} \sin \theta
\]
(positive, as it points in the \( +x \)-direction due to the symmetry).

3. Total \( x \)-component of the force on \( -q_1 \):
Adding the \( x \)-components of both forces, we get:
\[
F_x = F_{12x} + F_{13x} = \frac{k |q_1| q_2}{b^2} + \frac{k |q_1| |q_3|}{a^2} \sin \theta
\]

Final Answer
After dividing by \( k |q_1| \) to find the proportional relation, the \( x \)-component of the force on \( -q_1 \) is proportional to:
\[
\frac{q_2}{b^2} + \frac{q_3}{a^2} \sin \theta
\]